安徽省宿州市埇桥区2023-2024学年八年级上学期期中数学试题（北师大版）

试卷更新日期：2023-12-18 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题4分，满分40分）

1. 在平面内，下列说法不能确定物体位置的是（）

A、某影厅3排5座 B、北偏西30° C、某市解放路30号 D、东经110°，北纬30°

查看试题解析
2. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{13}$ B、 $\sqrt{27}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{16}$

查看试题解析
3. 若一个三角形的三边分别是7，24，25，则它的面积是（）

A、84 B、87.5 C、168 D、300

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{12} \div 3 = 2$ B、 $\sqrt{3} + \sqrt{3} = 3$ C、 $\sqrt{13} - \sqrt{3} = \sqrt{10}$ D、 $(\sqrt{3} + 1) (\sqrt{3} - 1) = 2$

查看试题解析
5. 如图，在平面直角坐标系中，被手挡住的点的坐标可能是（）

A、 $(- 1 ， - 3)$ B、 $(- 1 ， 3)$ C、 $(1 ， - 3)$ D、 $(1 ， 3)$

查看试题解析
6. 若函数 $y = (m + 1) x^{| m |} - 6$ 是一次函数，则m的值为（）

A、 $\pm 1$ B、 $- 1$ C、1 D、2

查看试题解析
7. 若点 $A (4 ， 3)$ 和点B是坐标平面内的两个点，且它们关于直线 $x = - 1$ 对称，则平面内点B的坐标为（）

A、 $(4 ， - 5)$ B、 $(3 ， 3)$ C、 $(- 6 ， 3)$ D、 $(- 6 ， 2)$

查看试题解析
8. 若a，b为实数，且 $\sqrt{a + 1} + {(9 - b)}^{2} = 0$ ，则 $\sqrt[3]{a + b}$ 的值为（）

A、 $- 2$ B、2 C、 $\pm 2$ D、3

查看试题解析
9. 若直线 $y = k x - b$ 经过一、二、三象限，则直线 $y = b x + k$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在长方体 $A B C D - E F G H$ 盒子中， $A B = 4 c m$ ， $B C = 3 c m$ ， $C G = 5 c m$ ，长为10cm的细直木棒IJ恰好从小孔G处插入，木棒的一端I与底面ABCD接触.当木棒的端点I在长方形ABCD内及边界运动时，GJ长度的最小值为（）

A、 $(10 - 5 \sqrt{2}) c m$ B、3cm C、 $(10 - 4 \sqrt{2}) c m$ D、5cm

查看试题解析

二、填空题（本大题共4小题，每小题5分，满分20分）

11. 若点 $P (m + 3 ， m + 4)$ 在y轴上，则点P的坐标为.

查看试题解析
12. 若点 $A (1 ， m)$ ， $B (2 ， n)$ 是直线 $y = - 2 x + 3$ 上的两点，则mn.（选填“>”“<”或“=”）

查看试题解析
13. 如图，在高 $B C = 3 m$ ，斜坡长 $A B = 5 m$ ，宽为2m的楼梯表面铺地毯，则地毯的面积至少需要 $m^{2}$ .

查看试题解析
14. 一次函数 $y = a x + b$ 在平面直角坐标系中的图象如图所示，化简 $| a + b | - \sqrt{{(b - a)}^{2}}$ 的结果是.

查看试题解析

三、（本大题共2小题，每小题8分，满分16分）

15. 计算： $(\sqrt{12} - \sqrt{\frac{8}{3}}) \times \sqrt{3} - (2 + \sqrt{3}) (2 - \sqrt{3}) + {(- 1)}^{2023}$ .

查看试题解析
16. 如图是北京市三所大学位置的平面示意图，图中小方格都是边长为1个单位长度的正方形.若清华大学的坐标为 $(0 ， 2)$ ，北京大学的坐标为 $(- 3 ， 1)$ .
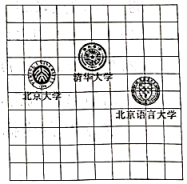
⑴请在图中画出相应的平面直角坐标系，并写出北京语言大学的坐标；
⑵若中国人民大学的坐标为 $(- 3 ， - 4)$ ，请在坐标系中标出中国人民大学的位置.

查看试题解析

四、（本大题共2小题，每小题8分，满分16分）

17. 某公司要印刷产品宣传材料，甲印刷厂提出：每份材料收1元印制费，另收1500元制版费；乙印刷厂提出：每份材料收2.5元印制费，不收制版费.

(1)、分别写出两印刷厂的收费y（元）与印制数量x（份）之间的关系式；

(2)、若该公司计划印制的宣传材料份数为1200份，请问该公司选择哪家印刷厂所付出的费用最少？

查看试题解析
18. 如图，数轴上的点A表示的数是 $- 1$ ，点B表示的数是1， $B C ⊥ A B$ 于点B，且 $B C = 2$ ，以点A为圆心，AC的长为半径画弧交数轴于点D，求点D表示的数.

查看试题解析

五、（本大题共2小题，每小题10分，满分20分）

19. 如图，点 $N (0 ， 6)$ ，点M在x轴的负半轴上， $O N = 3 O M$ ，点A为线段MN上一点， $A B ⊥ x$ 轴，垂足为点B， $A C ⊥ y$ 轴，垂足为点C.

(1)、求直线MN的表达式；

(2)、若点A的横坐标为 $- 1$ ，求四边形ABOC的面积.

查看试题解析
20. 在平面直角坐标系中有点 $M (m - 4 ， 2 m + 5)$ .

(1)、已知点 $N (5 ， 1)$ ，且 $M N ∥ y$ 轴，求点M的坐标；

(2)、已知点M到两坐标轴的距离相等，求点M的坐标，

查看试题解析

六、（本题满分12分）

21. 如图1，一次函数 $y = \frac{3}{4} x + 3$ 的图象与x轴相交于点A，与y轴相交于点B，点D是直线AB上的一个动点， $C D ⊥ x$ 轴于点C，点P是线段CD上的一个动点.

图1 图2

(1)、求A，B两点的坐标；

(2)、如图2，当点D在第一象限，且 $A B = B D$ 时，将 $△ A C P$ 沿着AP翻折，当点C的对应点 $C^{'}$ 落在直线AB上时，求点P的坐标.

查看试题解析

七、（本题满分12分）

22. 化简时，通常要求最终结果中分母不含有根号，观察下列等式：
① $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；
② $\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；
③ $\frac{1}{\sqrt{4} + \sqrt{3}} = \frac{\sqrt{4} - \sqrt{3}}{(\sqrt{4} + \sqrt{3}) (\sqrt{4} - \sqrt{3})} = \sqrt{4} - \sqrt{3} = 2 - \sqrt{3}$ ；
……
利用你观察到的规律解决下列问题：

(1)、化简 $\frac{1}{\sqrt{7} + \sqrt{6}}$ ；

(2)、求 $2 - \sqrt{3}$ 的倒数；

(3)、计算： $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + 2} + ⋯ + \frac{1}{\sqrt{99} + \sqrt{100}}$ .

查看试题解析

八、（本题满分14分）

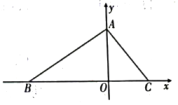
23. 如图，在平面直角坐标系中，O为坐标原点， $△ A B C$ 的边BC在x轴上，A，C两点的坐标分别为 $A (0 ， a)$ ， $C (b ， 0)$ ，点 $B (- 5 ， 0)$ ，且 ${(a - 4)}^{2024} = - | b - 3 |$ .已知点P从点B出发，以每秒2个单位的速度沿射线BO匀速运动，设点P的运动时间为ts.

备用图

(1)、求A，C两点的坐标；

(2)、连接PA，当点P在x轴的正半轴上时，用含t的代数式表示 $△ A O P$ 的面积

(3)、当点P在线段BO上运动时，在y轴上是否存在点Q，使 $△ P O Q$ 与 $△ A O C$ 全等？若存在，请求出t的值，并直接写出Q点的坐标；若不存在，请说明理由.

查看试题解析