安徽省淮南市田家庵区 2023-2024学年八年级上学期期中数学试题
试卷更新日期:2023-12-18 类型:期中考试
一、选择题(本大题共10小题,每小题4分,满分40分)
-
1. 如图,与关于直线l对称, , , 则的度数为( )
 A、30° B、50° C、80° D、100°2. 已知一个等腰三角形的两边长分别是2cm,4cm,则这个等腰三角形的周长是( )A、6cm B、8cm C、10cm D、8cm或10cm3. 下列手机屏幕手势解锁图案中,是轴对称图形的是( )A、
A、30° B、50° C、80° D、100°2. 已知一个等腰三角形的两边长分别是2cm,4cm,则这个等腰三角形的周长是( )A、6cm B、8cm C、10cm D、8cm或10cm3. 下列手机屏幕手势解锁图案中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图,在中,DE是AC的垂直平分线,若 , 的周长是15,则的周长为( )
4. 如图,在中,DE是AC的垂直平分线,若 , 的周长是15,则的周长为( ) A、19 B、17 C、15 D、135. 如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( ).
A、19 B、17 C、15 D、135. 如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( ).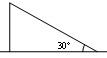 A、6米; B、9米; C、12米; D、15米.6. 如图,在中, , , 是的平分线,设和的面积分别是 , , 则的值为( )
A、6米; B、9米; C、12米; D、15米.6. 如图,在中, , , 是的平分线,设和的面积分别是 , , 则的值为( ) A、 B、 C、 D、7. 如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E的度数为( )
A、 B、 C、 D、7. 如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E的度数为( ) A、25° B、20° C、15° D、7.5°8. 如图, , , 则下列结论不一定正确的是( )
A、25° B、20° C、15° D、7.5°8. 如图, , , 则下列结论不一定正确的是( ) A、 B、 C、 D、9. 如图,小明用一副三角板拼成一幅“帆船图”, , , , , 连接AF,则的度数是( )
A、 B、 C、 D、9. 如图,小明用一副三角板拼成一幅“帆船图”, , , , , 连接AF,则的度数是( ) A、127.5° B、135° C、120° D、105°10. 如图,四边形ABCD中,AB=AD,点关于的对称点B′恰好落在CD上,若 , 则的度数为( )
A、127.5° B、135° C、120° D、105°10. 如图,四边形ABCD中,AB=AD,点关于的对称点B′恰好落在CD上,若 , 则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 如图,在中, , , . 若 , 则的度数为 .
 12. 如图,在 , , E是AB上一点,且 , 于点E,若 , 则的值为 .
12. 如图,在 , , E是AB上一点,且 , 于点E,若 , 则的值为 .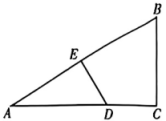 13. 如图,是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当的值最小时,的度数是 .
13. 如图,是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当的值最小时,的度数是 . 14. 如图,在中,AD平分 , 于点D,过点D作 , 交AB于点E.
14. 如图,在中,AD平分 , 于点D,过点D作 , 交AB于点E.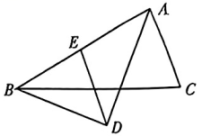 (1)、若 , 则DE的长为;(2)、若 , 则DE的长为 .
(1)、若 , 则DE的长为;(2)、若 , 则DE的长为 .三、(本大题共2小题,每小题8分,满分16分)
-
15. 如图,在平面直角坐标系中有一个 , 顶点 , , .

⑴将向右平移2个单位长度,再向下平移1个单位长度,作出平移后的;
⑵画出关于x轴对称的 , 并写出点的坐标.
16. 尺规作图(保留作图痕迹).如图,在内求作一点P,使P到两边的距离相等,且 .
四、(本大题共2小题,每小题8分,满分16分)
-
17. 如图,为等边三角形,交AC于点D,交AB于点E.
 (1)、求证:是等边三角形;(2)、求证: .18. 以点A为顶点作两个等腰直角三角形 , , 其中 , , 如图所示放置,D在AC边上,连接BD,CE.
(1)、求证:是等边三角形;(2)、求证: .18. 以点A为顶点作两个等腰直角三角形 , , 其中 , , 如图所示放置,D在AC边上,连接BD,CE. (1)、求证:;(2)、延长BD,交CE于点F,求的度数.
(1)、求证:;(2)、延长BD,交CE于点F,求的度数.五、(本大题共2小题,每小题10分,满分20分)
-
19. 为了解学生对所学知识的应用能力,某校老师在八年级数学兴趣小组活动中,设置了这样的问题:因为池塘两端A,B的距离无法直接测量,请同学们设计方案测量A,B的距离.甲、乙两位同学分别设计出了如下两种方案:
甲:如图1,先在平地上取一个可以直接到达点A,B的点O,连接AO并延长到点C,连接BO并延长到点D,使 , , 连接DC,测出DC的长即可;
乙:如图2,先确定直线AB,过点B作直线 , 在直线BE上找可以直接到达点A的一点D,连接DA,作 , 交直线AB于点C,最后测量BC的长即可.
甲、乙两个同学的方案是否可行?请说明理由.

图1 图2
20. 如图,在中,点D为AC边上一点,连接BD并延长到点E,过点E作交AC于点F,交AB于点G. (1)、若 , 求证:;(2)、若 , , , 求的度数.
(1)、若 , 求证:;(2)、若 , , , 求的度数.六、(本题满分12分)
-
21. 如图,在中, , .
 (1)、若 , , 求的度数;(2)、若 , 求的度数.
(1)、若 , , 求的度数;(2)、若 , 求的度数.七、(本题满分12分)
-
22. 如图,和都是边长为4厘米的等边三角形,两个动点P,Q同时从A点出发,点P以1厘米/秒的速度沿的方向运动,点Q以2厘米/秒的速度沿的方向运动,当点Q运动到点D时,P,Q两点同时停止运动.设P,Q运动的时间为t秒.
 (1)、点P,Q从出发到相遇所用时间是秒;(2)、当t取何值时,也是等边三角形?请说明理由;(3)、当时,判断PQ与AC的位置关系,请说明理由.
(1)、点P,Q从出发到相遇所用时间是秒;(2)、当t取何值时,也是等边三角形?请说明理由;(3)、当时,判断PQ与AC的位置关系,请说明理由.八、(本题满分14分)
-
23. 如图,在中, , AB的垂直平分线分别交AB,BC于点E,F,AC的垂直平分线分别交AC,BC于点M,N,直线EF,MN交于点P.
 (1)、求证:点P在线段BC的垂直平分线上;(2)、连接AP,求证:AP平分;(3)、设 , 其他条件不变时,求的度数.(用含的式子表示)
(1)、求证:点P在线段BC的垂直平分线上;(2)、连接AP,求证:AP平分;(3)、设 , 其他条件不变时,求的度数.(用含的式子表示)
-
-