山东省济南市天桥区2023-2024学年八年级上学期期中数学试题
试卷更新日期:2023-12-18 类型:期中考试
一、选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
-
1. 4的算术平方根是( )A、 B、2 C、-2 D、2. 下列各数中,是无理数的是( )A、3.1415926 B、 C、 D、3. 下列各点在第二象限的是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 已知点 , 在一次函数的图象上,则 , 的大小关系是( )A、 B、 C、 D、不能确定6. 已知为第四象限内的点,则一次函数的图象大致( )A、
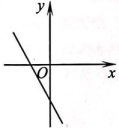 B、
B、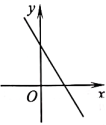 C、
C、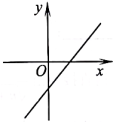 D、
D、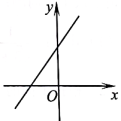 7. 已知是方程的解,那么m的值( )A、2 B、-2 C、4 D、-48. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
7. 已知是方程的解,那么m的值( )A、2 B、-2 C、4 D、-48. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A、 B、 C、 D、9. 如图,是直角三角形,点C在数轴上对应的数为-2,且 , , 若以点C为圆心,为半径画弧交数轴于点M , 则A , M两点间的距离为( )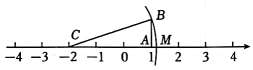 A、0.4 B、 C、 D、10. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
A、0.4 B、 C、 D、10. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,t=或 .
其中正确的结论有( )
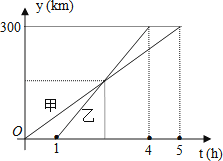 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题:(本大题共6个小题,每小题4分,共24分.)
-
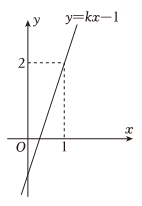
11. 电影票上“8排5号”记作 , 则“6排7号”记作.12. 比较大小:6.(填“”、“”或“”)13. 在平面直角坐标系中,已知点在x轴上,则点M的坐标为。14. 已知二元一次方程组则的值为15. 如图,函数的图象过点 , 则关于的方程的解是。
 16. 如图,在平面直角坐标系中,点B在x轴的正半轴上, , , , 点C , D均在边上,且 , 若的面积等于面积的三分之一,则点D的横坐标为.
16. 如图,在平面直角坐标系中,点B在x轴的正半轴上, , , , 点C , D均在边上,且 , 若的面积等于面积的三分之一,则点D的横坐标为.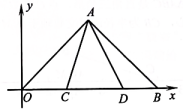
三、解答题(本大题10个小题,共86分.解答应写出文字说明、证明过程或演算步骤.)
-
17. 计算题(1)、;(2)、.18. 解方程组.19. 已知的立方根是2,的算术平方根是4,c是的整数部分.(1)、求a、b、c的值;(2)、求的平方根.20. “十一”期间,小华一家人开车到距家150千米的景点旅游,出发前,汽车油箱内储油35升,当行驶60千米时,发现油箱余油量为29升(假设行驶过程中汽车的耗油量均匀).(1)、求该车平均每千米的耗油量;(2)、写出余油量Q(升)与行驶路程x(千米)之间的关系式;(3)、当油箱中余油量低于3升时,汽车将自动报警,若往返途中不加油,他们能否在汽车报警前回到家?说明理由.21. 在如图所示的正方形网格中,每个小正方形的边长为1,格点(顶点是网格线的交点的三角形)的顶点A , C的坐标分别为 , .
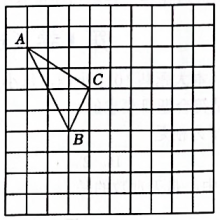
⑴请在如图所示的网格平面内作出平面直角坐标系;
⑵请作出关于y轴对称的;
⑶在y轴上存在一点P , 满足点P到点A与点B距离之和最小,请直接写出的最小值为 ▲ .
22. 阅读下面计算过程:
;
;
;
请解决下列问题:(1)、化简: ;
(2)、根据上面的规律,请直接写出 ;
(3)、利用上面的解法,请化简: .23. 第19届亚运于2023年9月23日至10月8日在杭州举行.某玩具店购进亚运会吉祥物“琮琮”、“莲莲”共100个,总费用为6600元,这两种吉祥物的进价、售价如表:
琮琮
莲莲
进价(元/个)
60
70
售价(元/个)
80
100
(1)、该玩具店购进“琮琮”和“莲莲”各多少个?(2)、后来该玩具店以60元/个的价格购进50个吉祥物“宸宸”,并以90元/个的价格售出,这家店将销售完这150个吉祥物所得利润的20%捐赠给了“希望工程”,求该玩具店捐赠了多少元?24. “漏壶”是一种古代计时器,在社会实践活动中,某小组同学根据“漏壶”的原理制作了如图①所示的液体漏壶,漏壶是由一个圆锥和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中,实验开始时圆柱容器中已有一部分液体.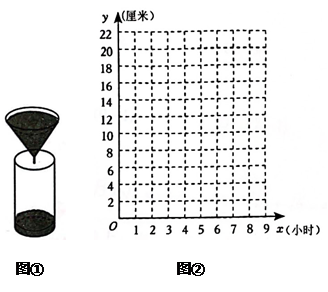 (1)、表是实验记录的圆柱体容器液面高度y(厘米)与时间x(小时)的数据:
(1)、表是实验记录的圆柱体容器液面高度y(厘米)与时间x(小时)的数据:时间x(小时)
1
2
3
4
5
圆柱体容器液面高度y(厘米)
6
10
14
18
22
在如图②所示的直角坐标系中描出上表的各点,并用线段连接.
(2)、请根据(1)中的数据确定y与x之间的函数表达式;(3)、如果本次实验记录的开始时间是上午9:00,那么当圆柱体容器液面高度达到12厘米时是几点?25. 如图1,直线:和直线与x轴分别相交于A , B两点,且两直线相交于点C , 直线l与y轴相交于点 , .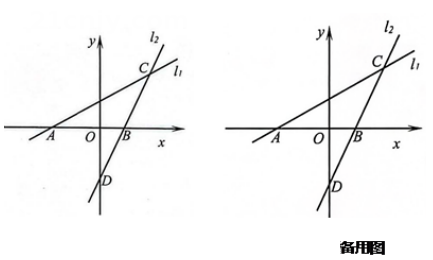 (1)、求点A的坐标及直线的函数表达式;(2)、求的面积;(3)、试探究在x轴上是否存在点P , 使得为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.26. 如图1,已知 , 以、为边分别向外作等边和等边 , 连接、 , 则有.
(1)、求点A的坐标及直线的函数表达式;(2)、求的面积;(3)、试探究在x轴上是否存在点P , 使得为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.26. 如图1,已知 , 以、为边分别向外作等边和等边 , 连接、 , 则有.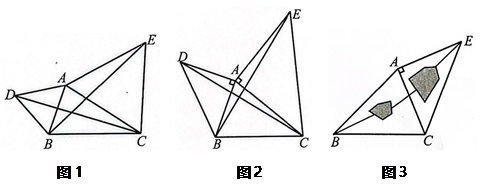 (1)、如图2,已知 , 以、为边分别向外作等腰直角三角形和等腰直角三角形 , 连接、 , 猜想与有什么数量关系?并说明理由.(2)、如图2,连接 , 若 , , , 求的值.(3)、运用图(1),图(2)中所积累的经验和知识,完成下题:如图(3),要测量池塘两岸相对的两点B、E的距离,已经测得 , , 米, , 求的长(结果保留根号).
(1)、如图2,已知 , 以、为边分别向外作等腰直角三角形和等腰直角三角形 , 连接、 , 猜想与有什么数量关系?并说明理由.(2)、如图2,连接 , 若 , , , 求的值.(3)、运用图(1),图(2)中所积累的经验和知识,完成下题:如图(3),要测量池塘两岸相对的两点B、E的距离,已经测得 , , 米, , 求的长(结果保留根号).