山东省济南市济阳区2023-2024学年八年级上学期期中数学试卷
试卷更新日期：2023-12-18 类型：期中考试
一、选择题。（本大题共10个小题，每小题4分，共40分）
-
1. 在平面直角坐标系中，点（3，﹣4）所在的象限是（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 如图，湖的两岸有A，C两点，在与AC成直角的BC方向上的点C处测得AB＝15米，BC＝12米，则A，C两点间的距离为（ ）
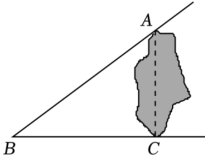A、3米 B、6米 C、9米 D、10米3. 在平面直角坐标系中，对于点P（x，y），我们把点P′（﹣y+1，x+1）叫做点P伴随点，已知点A1的伴随点为A2 ， 点A2的伴随点为A3 ， 点A3的伴随点为A4 ， …，这样依次得到点A1 ， A2 ， A3 ， …，An ， …若点A1的坐标为（2，4），则点A2023的坐标为（ ）A、（3，﹣1） B、（﹣2，﹣2） C、（﹣3，3） D、（2，4）4. 如图，△ABC和△ECD都是等腰直角三角形，△ABC的顶点A在△ECD的斜边DE上．下列结论：①△ACE≌△BCD；②∠DAB＝∠ACE；③AE+AC＝CD；④ED⊥BD；⑤AE2+AD2＝2AC2 ． 其中正确的有（ ）
A、2个 B、3个 C、4个 D、5 个二、填空题。（本大题共6个小题，每小题4分，共24分）
-
5.
如图，矩形OABC的边OA长为2，边AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交数轴于一点，则这个点表示的实数是
6. 如图，直线l1与x轴、y轴分别交于A（﹣2，0），B（0，6），直线l2经过点B且与x轴负半轴交于点C，∠ABC＝45°．若线段BC上存在一点P，使△ABP是以A为直角顶点的等腰直角三角形，则P点坐标为 ．
7. 如图，在△ABC中，AC＝5，BC＝12，AB＝13，将△ABC沿AD折叠，使点C落在AB上的点E处，则BD的长为 ．
三、解答题。（本大题共10个小题，共86分）
-
8. 一棵高8米的大树被折断，折断处A距地面的距离AC＝3米（点B为大树顶端着地处）．在大树倒下的方向停着一辆小轿车，小轿车距大树底部C的距离CD为4.5米，点D在CB的延长线上，求大树顶端着地处B到小轿车的距离BD．
9. 已知一次函数y＝2x﹣4．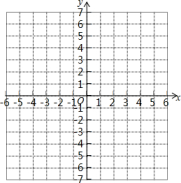
(1)、完成列表，并作出该函数的图象；(2)、设图象与x、y轴分别交于点A、B，求线段AB的长．10. 已知：如图，已知△ABC中，其中A（0，﹣2），B（2，﹣4），C（4，﹣1）.
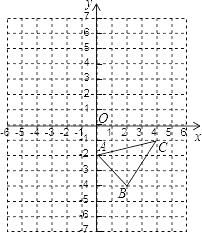(1)、画出与△ABC关于y轴对称的图形△A1B1C1；(2)、写出△A1B1C1各顶点坐标；(3)、求△ABC的面积.11. 如图，直线y＝kx+6与x轴、y轴分别相交于点E、F，点E的坐标为（﹣8，0），点A的坐标为（6，0），点P（x，y）是第一象限内的直线y＝kx+6上的一个动点．
(1)、求K的值；(2)、在点P的运动过程中，写出△OPA的面积S与x的函数表达式，并写出自变量x的取值范围；
(3)、探究，当点P运动到什么位置（求P的坐标）时，△OPA的面积是27．12. 如图，△ABC是等腰直角三角形，∠ACB＝90°，AC=BC=2 ， D在线段BC上，E是线段AD上一点．现以CE为直角边，C为直角顶点，在CE的下方作等腰直角△ECF，连接BF．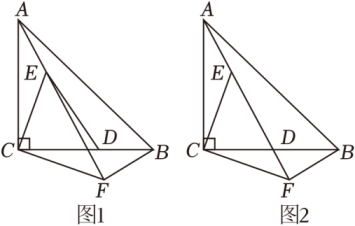
(1)、如图1，求证：∠CAE＝∠CBF；(2)、当A、E、F三点共线时，如图2，①求证：∠DFB＝90°；
②若BF＝2，求AF的长．