安徽省宿州市埇桥区教育集团2023-2024学年八年级上学期期中数学试题

试卷更新日期：2023-12-18 类型：期中考试

进入出卷网下载

一、选择题（每小题2分，共20分）

1. $- 8$ 的立方根是（）

A、 $- 2$ B、2 C、 $\pm 2$ D、4

查看试题解析
2. 下列长度的三条线段不能组成直角三角形的是（）

A、3，5，7 B、6，8，10 C、5，12，13 D、1，2， $\sqrt{3}$

查看试题解析
3. 点 $P$ 在第二象限内，且 $P$ 到 $x$ 轴的距离是4，到 $y$ 轴的距离是3，那么点 $P$ 的坐标为（）

A、 $(- 4 ， 3)$ B、 $(4 ， - 3)$ C、 $(- 3 ， 4)$ D、 $(3 ， - 4)$

查看试题解析
4. 下列各数：3.14159，2018，0.13113111311113…， $- π$ ， 5， $\frac{22}{7}$ .其中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 下列语句：①任意一个数都有两个平方根；② $- 1$ 是1的平方根；③带根号的数都是无理数；④ $\sqrt{81}$ 的平方根是 $\pm 3$ ；⑤ ${(- 2)}^{2}$ 的算术平方根2.其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 一次函数 $y = \frac{1}{2} x + 1$ 的图象与 $y$ 轴、 $x$ 轴形成的三角形的面积为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 已知两个一次函数 $y_{1} = a x + b$ 与 $y_{2} = b x + a$ ，它们在同一平面直角坐标系中的图象可能是下列选项中的（）

A、 B、 C、 D、

查看试题解析
8. 已知点 $(- 4 ， y_{1})$ ， $(2 ， y_{2})$ 都在直线 $y = - \frac{2}{3} x + b$ 上，则 $y_{1}$ 与 $y_{2}$ 的大小关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、不能确定

查看试题解析
9. 已知 $\sqrt{{(2 a - 1)}^{2}} = 1 - 2 a$ ，那么 $a$ 的取值范围是（）

A、 $a > \frac{1}{2}$ B、 $a < \frac{1}{2}$ C、 $a \geq \frac{1}{2}$ D、 $a \leq \frac{1}{2}$

查看试题解析
10. 如图，在△ABC中，∠ACB＝90°，分别以点A和点B为圆心，以相同的长（大于 $\frac{1}{2}$ AB）为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交BC于点E．若AC＝3，AB＝5，则DE等于（）

A、2 B、 $\frac{10}{3}$ C、 $\frac{15}{8}$ D、 $\frac{15}{2}$

查看试题解析

二、填空题：（每小题3分，共18分）

11. 16的算术平方根是

查看试题解析
12. 若点 $A (1 - m ， 3)$ 与点 $B (2 ， 1 + n)$ 关于 $x$ 轴对称，则 $2 m + n =$ .

查看试题解析
13. 若 $y = \sqrt{3 - x} + \sqrt{x - 3} + 4$ ，则 $x^{2} + y^{2}$ 的平方根是.

查看试题解析
14. 如图，数轴上点A表示的实数是.

查看试题解析
15. 已知 $y$ 与 $x + 1$ 成正比例，当 $x = 1$ 时， $y = 4$ ，则当 $x = 2$ 时， $y$ 的值是.

查看试题解析
16. 如图，动点 $P$ 在平面直角坐标系中按图中简头所示方向运动，第1次从原点运动到点 $(1 ， 1)$ ，第2次运动到点 $(2 ， 0)$ ，第3次运动到点 $(3 ， - 1)$ ， …，按照这样的运动规律，点 $P$ 第17次运动到的点的坐标为.

查看试题解析

三、解答题：

17. 计算：

(1)、 $(1 - \sqrt{2})^{0} + | 2 - \sqrt{5} | + (- 1)^{2020} - \frac{1}{3} \times \sqrt{45}$ .

(2)、 $(\sqrt{3} - 2) (\sqrt{3} + 1) + \sqrt{15} \div \sqrt{5}$ .

查看试题解析
18. 甲、乙两车从A城出发沿一条笔直公路匀速行驶至B城.在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示.

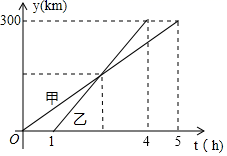(1)、A，B两城相距千米，乙车比甲车早到小时；

(2)、甲车出发多长时间与乙车相遇？

(3)、若两车相距不超过30千米时可以通过无线电相互通话，则两车都在行驶过程中可以通过无线电通话的时间有多长？

查看试题解析
19. 在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系，已知格点三角形 $A B C$ （三角形的三个顶点都在小正方形的顶点上）.
⑴画出 $△ A B C$ 关于 $y$ 轴对称的 $△ A_{1} B_{1} C_{1}$ ；
⑵写出点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 的坐标；
⑶在 $y$ 轴上找 $D$ 点，使 $B D + C D$ 最小，请你标出点 $D$ 的位置并直接写出点 $D$ 的坐标.

查看试题解析
20. 观察右图，认真分析各式，然后解答问题.
$O A_{2}^{2} = {(\sqrt{1})}^{2} + 1 = 2$ ， $S_{1} = \frac{\sqrt{1}}{2}$ ；
$O A_{3}^{2} = {(\sqrt{2})}^{2} + 1 = 3$ ， $S_{2} = \frac{\sqrt{2}}{2}$ ；
$O A_{4}^{2} = {(\sqrt{3})}^{2} + 1 = 4$ ， $S_{3} = \frac{\sqrt{3}}{2}$ …

(1)、请用含有 $n$ （ $n$ 为正整数）的等式 $S_{n} =$ ；

(2)、推算出 $O A_{10} =$ .

(3)、求出 $S_{1}^{2} + S_{2}^{2} + S_{3}^{2} + \dots \dots + S_{10}^{2}$ 的值.

查看试题解析
21. 某校八年级（1）班的小华和小轩学习了“勾股定理”之后，为了测得风筝的垂直高度 $C E$ ，他们进行了如下操作：①测得水平距离 $B D$ 的长为12米；②根据手中剩余线的长度计算出风筝线 $B C$ 的长为20米；③牵线放风筝的小明的身高为1.62米.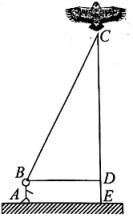

(1)、求风筝的垂直高度 $C E$ ；

(2)、如果小明想风筝沿 $C D$ 方向下降11米，则他应该往回收线多少米？

查看试题解析
22. 阅读下列材料，解答后面的问题：
$\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - 1$ ；
$\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{2 + \sqrt{3}} = 2 - 1 = 1$ ；
$\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{2 + \sqrt{3}} + \frac{1}{\sqrt{5} + 2} = \sqrt{5} - 1$ ；

(1)、写出下一个等式；

(2)、计算 $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{2 + \sqrt{3}} + \dots \dots + \frac{1}{\sqrt{100} + \sqrt{99}}$ 的值；

(3)、请求出 $(\frac{1}{\sqrt{101} + \sqrt{100}} + \frac{1}{\sqrt{102} + \sqrt{101}} + \dots \dots + \frac{1}{\sqrt{2122} + \sqrt{2121}}) \times (\sqrt{2122} + \sqrt{100})$ 的运算结果.

查看试题解析
23. 如图，已知直线 $y = - \frac{1}{3} x + 1$ 与 $x$ 轴、 $y$ 轴分别交于 $A$ 、 $B$ 两点，以线段 $A B$ 为直角边在第一象限内作等腰 $R t △ A B C$ ， $∠ B A C = 90 °$ ，点 $P$ 为直线 $B C$ 上一个动点.

(1)、 $A$ 点坐标为， $B$ 点坐标为；

(2)、求直线 $B C$ 的解析式；

(3)、当 $S_{△ A O P} = 3 S_{△ A O B}$ 时，求点 $P$ 的坐标.

查看试题解析