河北省张家口市宣化区2023-2024学年八年级上学期期中数学试题
试卷更新日期:2023-12-18 类型:期中考试
一、选择题:(本大题有14个小题,1-6小题每题3分,7-14小题每题2分,共34分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 下列各组中的两个图形属于全等图形的是( )A、
 B、
B、 C、
C、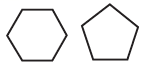 D、
D、 2. 如图,将绕点逆时针旋转到 , 点恰好落在边上. 已知 , 则的长是( )
2. 如图,将绕点逆时针旋转到 , 点恰好落在边上. 已知 , 则的长是( )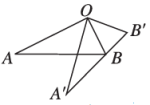 A、 B、 C、 D、3. 约分的结果是( )A、3x B、3xy C、 D、4. 如图,点在的边上,用尺规作出了 , 连接 , 作图痕迹中,根据的是( )
A、 B、 C、 D、3. 约分的结果是( )A、3x B、3xy C、 D、4. 如图,点在的边上,用尺规作出了 , 连接 , 作图痕迹中,根据的是( )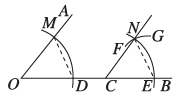 A、 B、 C、 D、5. 如图,是四个村庄,在一条东西走向公路的沿线上, , , 村庄和 , 和间也有公路相连,且公路是南北走向, , 只有和之间由于间隔了一个小湖,无直接相连的公路. 现决定在湖面上造一座桥,测得 , 则建造的桥长至少为( )
A、 B、 C、 D、5. 如图,是四个村庄,在一条东西走向公路的沿线上, , , 村庄和 , 和间也有公路相连,且公路是南北走向, , 只有和之间由于间隔了一个小湖,无直接相连的公路. 现决定在湖面上造一座桥,测得 , 则建造的桥长至少为( )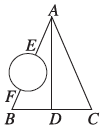 A、 B、 C、 D、6. 小明在纸上书写了一个正确的演算过程,同桌小亮一不小心撕坏了一角,如图所示,则撕坏的一角中“
A、 B、 C、 D、6. 小明在纸上书写了一个正确的演算过程,同桌小亮一不小心撕坏了一角,如图所示,则撕坏的一角中“ ”为( )
”为( )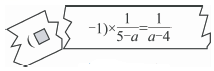 A、 B、 C、 D、7. 如图,在正方形中,为边上一点,点在边上,且 , 将点绕着点顺时针旋转 , 得到点 , 连接 , 则的最小值为( )
A、 B、 C、 D、7. 如图,在正方形中,为边上一点,点在边上,且 , 将点绕着点顺时针旋转 , 得到点 , 连接 , 则的最小值为( )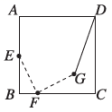 A、2 B、 C、3 D、
A、2 B、 C、3 D、二、填空题:(本大题共6个小题,每小题3分,共18分. 把答案写在题中横线上)
-
8. 若分式的值为零,则为.9. 分式和的最简公分母为.10. 已知 , ,则 与 的大小关系为.11. 已知和 , 已知 , 则.12. 关于的分式方程有增根,则 .13. 如图,在数轴上竖直摆放一个直径为4个单位长度的半圆,是半圆上的中点,半圆直径的一个端点位于原点. 该半圆沿数轴从原点开始向右无滑动滚动,当点第一次落在数轴上时,此时点表示的数为.
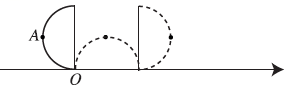
三、解答题:(本大题共6个小题,共48分. 解答应写出文字说明、证明过程或演算步骤)
-
14. 如图,池塘两端的距离无法直接测量,请同学们设计测量之间距离的方案.
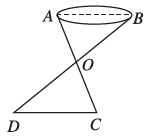
小明设计的方案如图所示:他先在平地上选取一个可以直接到达的点 , 然后连接和 , 接着分别延长和并且使 , 最后连接 , 测出的长即可.
你认为以上方案可行吗?若可行,请说明理由.
15. 如图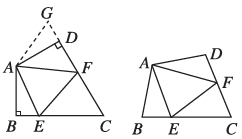
图1 图2
(1)、问题背景:如图1,在四边形中,分别是上的点,且 , 探究图中线段之间的数量关系. 小王同学探究此问题的方法是,延长到点. 使. 连接 , 先证明 , 再证明 , 可得出结论,他的结论应是;(2)、探索延伸:如图2,若在四边形中,分别是上的点,且 , 上述结论是否仍然成立?若成立请说明理由.16. 点在数轴上分别表示有理数两点之间的距离表示为 , 在数轴上两点之间的距离.已知数轴上两点对应的数分别为、3,点为数轴上一动点,其对应的数为.
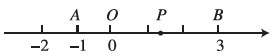 (1)、两点之间的距离是;(2)、设点在数轴上表示的数为 , 则与之间的距离表示为;(3)、若点到点、点的距离相等,则点对应的数为;(4)、数轴上是否存在点 , 使点到点、点的距离之和为8?若存在,请直接写出的值;若不存在,说明理由.
(1)、两点之间的距离是;(2)、设点在数轴上表示的数为 , 则与之间的距离表示为;(3)、若点到点、点的距离相等,则点对应的数为;(4)、数轴上是否存在点 , 使点到点、点的距离之和为8?若存在,请直接写出的值;若不存在,说明理由.