河北省张家口市宣化区2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-18 类型:期中考试
一、选择题(本大题共12小题,每小题2分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 下列方程中是一元二次方程的是( )A、 B、 C、 D、2. 一元二次方程二次项系数、一次项系数、常数项分别为( )A、6,2,9 B、2,-6,9 C、2,-6,-9 D、-2,6,-93. 若关于的一元二次方程有实数根,则的取值范围是( )A、且 B、 C、 D、且4. 若a是方程的一个解,则的值是( )A、2023 B、-2023 C、2022 D、-20225. 抛物线向右平移3个单位长度得到的抛物线的函数关系式为( )A、 B、 C、 D、6. 我国南宋数学家杨辉所著的《田亩比类乘除捷法》中有这样一道题:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?”意思是:一块矩形田地的面积为864平方步,只知道它的宽比长少12步,问它的长和宽各多少步?设这块田地的宽为x步,则正确的是( )A、依题意 B、依题意 C、这块田地的宽为24步或36步 D、这块田地的周长为120步7. 在同一平面直角坐标系中,一次函数 和二次函数 的图象大致为( )A、
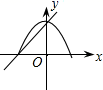 B、
B、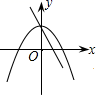 C、
C、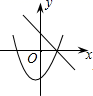 D、
D、 8. 已知抛物线的位置如图所示,甲、乙、丙三人关于x的一元二次方程的根的情况判断如下,其中正确的有( )
8. 已知抛物线的位置如图所示,甲、乙、丙三人关于x的一元二次方程的根的情况判断如下,其中正确的有( )甲:当时,该方程没有实数根;
乙:当时,该方程有两个相等实数根;
丙:当时,该方程有两个不相等的实数根.
 A、0个 B、1个 C、2个 D、3个9. 老师设计了接力游戏,用合作的方式完成配方法求抛物线的顶点坐标,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成求解.过程如图所示:
A、0个 B、1个 C、2个 D、3个9. 老师设计了接力游戏,用合作的方式完成配方法求抛物线的顶点坐标,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成求解.过程如图所示: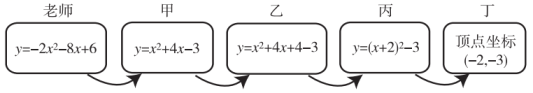
接力中,自己负责的出现错误的是( )
A、甲和乙 B、乙和丙 C、乙和丁 D、甲和丙10. 如图是二次函数的部分图象,图象过点 , 对称轴为直线 , 给出四个结论:①;②;③;④若点、为函数图象上的两点,则 , 其中正确结论是( ) A、①④ B、②③ C、①③ D、②④11. 题目:“如图,抛物线与直线相交于点和点B.点M是直线AB上的一个动点,将点M向左平移3个单位长度得到点N,若线段MN与抛物线只有一个公共点,直接写出点M的横坐标的取值范围.”对于其答案,甲答: , 乙答: , 丙答: , 丁答: , 则正确的是( )
A、①④ B、②③ C、①③ D、②④11. 题目:“如图,抛物线与直线相交于点和点B.点M是直线AB上的一个动点,将点M向左平移3个单位长度得到点N,若线段MN与抛物线只有一个公共点,直接写出点M的横坐标的取值范围.”对于其答案,甲答: , 乙答: , 丙答: , 丁答: , 则正确的是( )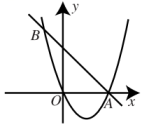 A、只有甲答的对 B、甲、乙答案合在一起才完整 C、甲、丙答案合在一起才完整 D、甲、丁答案合在一起才完整
A、只有甲答的对 B、甲、乙答案合在一起才完整 C、甲、丙答案合在一起才完整 D、甲、丁答案合在一起才完整二、填空题(本大题共6小题,每小题3分,共18分.把答案写在题中横线上)
-
12. 关于x的方程是一元二次方程,则.13. 已知a,b分别是方程的两根,则的值为.14. 某种传染病,若有一人感染,经过两轮传染后将共有49人感染.设这种传染病每轮传染中平均一个人传染了x个人,列出方程为.15. 如果实数a,b满足 , , 且 , 则ab的值.16. 如图是抛物线型拱桥,当拱顶离水面3m时,水面宽4m,水面上升2m,水面宽度减少m.
 17. 如图,在平面直角坐标系中,正方形ABCD的顶点A、B、C的坐标分别为、、.若抛物线的图象与正方形ABCD有公共点,则a的取值范围是.
17. 如图,在平面直角坐标系中,正方形ABCD的顶点A、B、C的坐标分别为、、.若抛物线的图象与正方形ABCD有公共点,则a的取值范围是.
三、解答题(共7小题,共58分)
-
18. 选择适当的方法解方程.(1)、(2)、19. 台风“杜苏芮”牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动,第一天收到捐款3000元,第三天收到捐款4320元.(1)、如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)、按照(1)中收到的捐款的增长速度,第四天该单位能收到多少捐款?20. 在实数范围内定义新运算“”,其规则为: , 根据这个规则,解决下列问题:(1)、求中的x值;(2)、证明:中,无论m为何值,x总有两个不同的值.21. 如图,某单位拟在一块空地上修建矩形植物园ABCD,其中一边靠墙,可利用的墙长不超过16米,另外三边由36米长的栅栏围成,设矩形ABCD中,垂直于墙的边米,面积为y平方米.
 (1)、y与x之间的函数关系式为 , 自变量x的取值范围为;(2)、若矩形ABCD的面积为154平方米,求x的值;(3)、当矩形ABCD的面积最大时,利用的墙长是多少米?并求此时的最大面积.22. 已知抛物线如图所示,它与x轴的一个交点的坐标为 , 与y轴的交点坐标为.
(1)、y与x之间的函数关系式为 , 自变量x的取值范围为;(2)、若矩形ABCD的面积为154平方米,求x的值;(3)、当矩形ABCD的面积最大时,利用的墙长是多少米?并求此时的最大面积.22. 已知抛物线如图所示,它与x轴的一个交点的坐标为 , 与y轴的交点坐标为.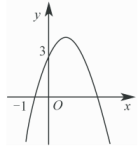 (1)、求抛物线对应的函数表达式及与x轴的另一个交点B的坐标;(2)、根据图象回答:当x取何值时,;(3)、在抛物线的对称轴上有一动点P,求的最小值,并求当取最小值时点P的坐标.23. 某商场经营某种品牌的玩具,购进时的单价是30元,经市场预测,销售单价为40元时,可售出600个;而销售单价每涨1元,销售量将减少10个,设每个销售单价为x元.(1)、写出销售量y(件)和获得利润w(元)与销售单价x(元)之间的函数关系;(2)、若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?24. 已知抛物线L:的顶点为C.(1)、求点C的坐标;(2)、已知点和点 , 且PQ的中点恰好在y轴上.
(1)、求抛物线对应的函数表达式及与x轴的另一个交点B的坐标;(2)、根据图象回答:当x取何值时,;(3)、在抛物线的对称轴上有一动点P,求的最小值,并求当取最小值时点P的坐标.23. 某商场经营某种品牌的玩具,购进时的单价是30元,经市场预测,销售单价为40元时,可售出600个;而销售单价每涨1元,销售量将减少10个,设每个销售单价为x元.(1)、写出销售量y(件)和获得利润w(元)与销售单价x(元)之间的函数关系;(2)、若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?24. 已知抛物线L:的顶点为C.(1)、求点C的坐标;(2)、已知点和点 , 且PQ的中点恰好在y轴上.① ▲ ;
②当时,若抛物线L平移后经过点P,Q,设平移后的抛物线为 , 求L平移到的最短路程.