河北省唐山市遵化市2023-2024学年八年级上学期期中数学试题

试卷更新日期：2023-12-18 类型：期中考试

进入出卷网下载

一、选择题（本题1-10小题各3分，11-16小题各2分，共42分）

1. 下列是无理数的是（）.

A、 $- 5$ B、 $\sqrt{16}$ C、 $\sqrt[3]{10}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列约分不正确的是（）

A、 $\frac{x^{3}}{x^{2}} = x$ B、 $\frac{a^{2}}{2 a} = 1$ C、 $\frac{m n}{m n^{2}} = \frac{1}{n}$ D、 $\frac{- x + y}{x - y} = - 1$

查看试题解析
3. 如图， $A B = A C$ ， $A F = A E$ ， $∠ B = 2 5^{∘}$ ，则 $∠ C =$ （）.

A、 $2 5^{∘}$ B、 $3 0^{∘}$ C、 $4 5^{∘}$ D、 $6 0^{∘}$

查看试题解析
4. 下列说法正确的是（）.

A、1是1的平方根 B、1的平方根是1 C、 $(- 3)^{2}$ 的平方根是 $- 3$ D、 $- 1$ 没有立方根

查看试题解析
5. 有如下计算过程：
$\frac{1}{9 a^{2} + 6 a + 1} - \frac{1}{3 a + 1}$
$= \frac{1}{(3 a + 1)^{2}} - \frac{3 a + 1}{(3 a + 1)^{2}}$ 第（1）步
$= \frac{1 - 3 a + 1}{(3 a + 1)}$ 第（2）步
$= \frac{2 - 3 a}{(3 a + 1)^{2}}$ 第（3）步
其中出现错误的步骤是（）.

A、第（1）步 B、第（2）步 C、第（3）步 D、没有错误

查看试题解析
6. 下列有逆定理的是（）.

A、直角都相等 B、两直线平行，同旁内角互补 C、对顶角相等 D、全等三角形的对应角相等

查看试题解析
7. 如图是作 $△ A B C$ 的作图痕迹，则此作图的已知条件是（）.

A、已知三角形的三边 B、已知三角形的两边及夹角 C、已知三角形的两角及夹边 D、已知三角形的两角及一角的对边

查看试题解析
8. 若 $x < \sqrt{19} + 3 < x + 1$ ，则 $x$ 可取的整数值有（）.

A、9 B、8 C、7 D、7或8

查看试题解析
9. 如图所示， $A D = B E$ ，若要使 $△ A C B ≅ △ D F E$ ，可添加条件：
① $A C = D F$ ， $B C = E F$ ② $C A / / D F$ ， $C B / / E F$ ③ $∠ C = ∠ F$ ， $A C / / D F$ ④ $A C = D F$ ， $B C / / E F$ 其中正确的有（）.

A、①② B、①③ C、①②③ D、①②③④

查看试题解析
10. 下列各数： $- \sqrt{0.1}$ ， $- \sqrt[3]{- 6}$ ， $1 - \sqrt{3}$ ， $\sqrt{(- 2)^{2}}$ ， $\frac{π}{3} - 1.2$ ， $\sqrt[3]{0}$ ，绝对值为它相反数的数有（）个.

A、3个 B、4个 C、5个 D、6个

查看试题解析
11. 如图所示，在 $△ A B C$ 中， $D$ 、 $E$ 分别是 $A B$ 、 $A C$ 的中点， $C F / / A B$ ，交 $D E$ 的延长线于点 $F$ ，则下列说法错误的是（）.

A、 $D B = C F$ B、 $E$ 是线段 $D F$ 的中点 C、将 $△ E C F$ 绕点 $E$ 旋转 $18 0^{∘}$ 可与 $△ E A D$ 重合 D、 $△ A D E ≌ △ C F E$ ，且证明 $△ A D E$ 与 $△ C F E$ 全等只能用判定定理“ASA”

查看试题解析
12. 甲、乙、丙三人对平方根和立方根进行了研究，以下是他们三人的结论：
甲：当 $a > 0$ 时， $\sqrt{a^{2}} = a$ 乙： $a < 0$ 时， $- \sqrt{a^{2}} = - a$ 丙：当 $a > 0$ 时， $\sqrt[3]{- a} = - \sqrt[3]{a}$ 则下列说法正确的是（）.

A、只有甲、乙正确 B、只有甲、丙正确 C、甲、乙、丙都正确 D、甲、乙、丙都不正确

查看试题解析
13. 遵化市沙石峪人民创造了“万里千担一亩田，羙石板上创高产”的奇迹，沙石峪人民被周恩来同志誉为“当代愚公”，为激励后人传承和发扬“当代思公”的光荣传统和优良作风，建造了沙石峪纪念馆，2019年沙石峪纪念馆被中宣部授予“全国爱国主义教育示范基地”。五四青年节，学校的八年级学生去距学校 $10 K m$ 的沙石峪纪念馆参观，一部分学生骑自行车先走，过了 $15 m i n$ 后，其余学生乘汽车出发，结果他们同时到达，已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为 $x k m / h$ ，则所列方程正确的是（）.

A、 $\frac{10}{x} - \frac{10}{2 x} = 15$ B、 $\frac{10}{2 x} - \frac{10}{x} = 15$ C、 $\frac{10}{x} - \frac{10}{2 x} = \frac{1}{4}$ D、 $\frac{10}{2 x} - \frac{10}{x} = \frac{1}{4}$

查看试题解析
14. 如图，是工人师傅用同一种材料制成的金属框架，已知 $∠ B = ∠ E$ ， $A B = D E$ ， $B F = E C$ ，其中 $△ A B C$ 的周长为24cm， $C F = 3 c m$ ，则制成整个金属框架所需这种材料的总长度为（）

A、45cm B、48cm C、51cm D、54cm

查看试题解析
15. 已知一个三角形三边长分别为 $6 ， 8 ， a$ ，且关于 $y$ 的分式方程 $\frac{y + 3 a}{y - 3} + \frac{4 a}{3 - y} = 2$ 的解是非负数，则符合条件的所有整数 $a$ 的和为（）.

A、20 B、18 C、17 D、15

查看试题解析
16. 如图，在四边形 $A B C D$ 中， $A D / / B C$ ，若 $∠ D A B$ 的平分线 $A E$ 交 $C D$ 于点 $E$ ，连接 $B E$ ，且 $B E$ 平分 $∠ A B C$ ，则下列结论：① $∠ A E B = 9 0^{∘}$ ；② $E$ 为 $C D$ 的中点；③ $B C + A D = A B$ ；④ $S_{△ A B E} = \frac{1}{2} S_{□ A B C D}$ ，其中正确的是（）.

A、①②③ B、①③④ C、②③④ D、①②③④

查看试题解析

二、填空（共3小题，每题3分，共9分）.

17. 已知 $2 x^{2} - 1 = 9$ ；则 $x$ 的值为.

查看试题解析
18. 若 $\frac{1}{a} - \frac{1}{b} = 4$ ，计算下列各式的值：

(1)、 $\frac{a b}{a - b} =$ ；

(2)、 $\frac{a - b}{3 a + 2 a b - 3 b} =$ .

查看试题解析
19. 如图，在直角三角形 $A B C$ 中， $∠ B = 9 0^{∘}$ ， $A B = 5 c m$ ， $B C = 6 c m$ ，点 $P$ 从点 $B$ 开始沿 $B A$ 以 $1 c m / s$ 的速度向点运动，同时，点 $Q$ 从点 $B$ 开始沿 $B C$ 以 $2 c m / s$ 的速度向点 $C$ 运动.当 $t =$ 时，四边形 $A C Q P$ 的面积为 $△ P Q B$ 面积的 $\frac{2}{3}$ .

查看试题解析

三、解答题（共69分）.

20. 计算：

(1)、 $4 \sqrt{5} + \sqrt{45} - 4 \sqrt{2} \div \sqrt{8}$ ；

(2)、 ${(\sqrt{2} + 1)}^{2} - (\sqrt{3} + 1) (\sqrt{3} - 1)$ ．

查看试题解析
21. 如图，已知点 $B$ ， $F$ ， $C$ ， $E$ 在直线上，点 $A$ ， $D$ 在异侧，且 $A C / / D F$ ， $A C = D F$ .

(1)、请你添加一个适当的条件：使得 $△ A B C ≌ △ D E F$ .结合所添加的条件证明 $△ A B C ≌ △ D E F$ ；

(2)、在（1）的条件下，若 $B E = 20$ ， $B F = 6$ ，求 $F C$ 的长度.

查看试题解析
22. 小明邀请你参与数学接龙游戏：
【问题】解分式方程： $\frac{3 x}{x - 1} + \frac{x - 1}{3 x} = 2$
【小明解答的部分】解：设 $\frac{3 x}{x - 1} = t$ ，则 $\frac{x - 1}{3 x} = \frac{1}{t}$ 故原方程可化为 $t + \frac{1}{t} = 2$ ，去分母并移项，得 $t^{2} - 2 t + 1 = 0$
【接龙】

查看试题解析
23. 如图， $△ A B C$ 和 $△ A D E$ 中， $A C = A E$ ， $∠ B = ∠ D$ ， $∠ B A D = ∠ C A E$ ，边 $A D$ 与边 $B C$ 交于点 $M$ （不与 $B$ 、 $C$ 重合），点 $B$ 、 $E$ 在 $A D$ 异侧；

(1)、求证 $△ B A C ≌ △ D A E$ ；

(2)、若 $∠ B = ∠ B A D = \frac{1}{2} ∠ D A C$ ， $∠ C = ∠ A M C$ ，求 $∠ A E D$ 的度数.

查看试题解析
24. 一小船由 $A$ 港顺流而下到 $B$ 港需 $6 h$ ，由 $B$ 港逆流而上到 $A$ 港需 $8 h$ .某天早晨6点，该船由 $A$ 港出发驶向 $B$ 港，到达 $B$ 港时，发现船上一救生圈在途中掉入水中，于是立刻返回，Ih后遇到救生圈.

(1)、该船按水流速度由A港漂流到B港需要多少小时？

(2)、救生圈是何时掉入水中的？

查看试题解析
25. 如图，将面积分别为2和3的两个正方形放在数轴上，使正方形一个顶点和原点 $O$ 重合，一条边恰好落在数轴上，其另一个顶点分别为数轴上的点 $A$ 和点 $B$ ，

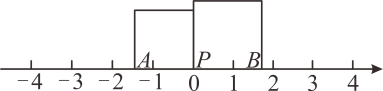(1)、点 $A$ 表示的数为；点B表示的数为，线段 $A B$ 的长度为；

(2)、一只蚂蚁从点 $A$ 沿数轴向右爬了2个单位长度到达点 $C$ ，设点 $C$ 表示的数为 $c$ ，
①实数 $c$ 的值为 ▲ ；
②求 $| c + 1 | + | c - 1 |$ 的值；

(3)、在数轴上，还有 $D$ 、 $E$ 两点分别表示 $m$ ， $n$ 且有 $| 2 m + n |$ 与 $\sqrt{n^{2} - 16}$ 互为相反数，求 $2 m - 3 n$ 的平方根。

查看试题解析
26. 如下是某书中某一页的部分内容：
如图，在 $△ A B C$ 中， $D$ 是边 $B C$ 的中点，过点 $C$ 画直线 $C E$ ，使 $C E / / A B$ ，交 $A D$ 的延长线于点 $E$ ，求证： $A D = E D$ .
证明： $∵ C E / / A B$ （已知）
$∴ ∠ A B D = ∠ E C D$ ， $∠ B A D = ∠ C E D$ （两直线平行，内错角相等）.
在 $△ A B D$ 与 $△ E C D$ 中，
$∵ ∠ B A D = ∠ C E D$ ， $∠ A B D = ∠ E C D$ （已证），
$B D = C D$ （已知），
$∴ △ A B D ≌ △ E C D (A A S)$ ，
$∴ A D = E D$ （全等三角形的对应边相等）.
图（1）图（2）图（3）

(1)、【方法应用】如图（1），在 $△ A B C$ 中， $A B = 6 ， A C = 4$ ，则 $B C$ 边上的中线 $A D$ 长度的取值范围是；

(2)、【猜想证明】如图（2），在四边形 $A B C D$ 中， $A B / / C D$ ，点 $E$ 是 $B C$ 的中点，若 $A E$ 是 $∠ B A D$ 的平分线，试猜想线段 $A B$ ， $A D$ ， $D C$ 之间的数量关系，并证明你的猜想.

(3)、【拓展延伸】如图（3），已知 $A B / / C F$ ，点 $E$ 是 $B C$ 的中点，点 $D$ 在线段 $A E$ 上， $∠ E D F = ∠ B A E$ ，若 $A B = 5$ ， $C F = 2$ ，直接写出线段 $D F$ 的长。

查看试题解析