河北省唐山市遵化市2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-18 类型:期中考试
一、选择题:(本大题共16个小题,共38分.1-6小题各3分,7-16小题各2分.每小题只有一项符合题目要求)
-
1. 下列方程中①②③④是一元二次方程的( )A、①和② B、②和③ C、③和④ D、①和③2. 5名同学参加市级作文比赛,老师只公布了其中4人的成绩,分别88分,80分,75分,82分,没有公布小红的成绩,但告诉大家5个人的平均成绩为84分.小红得的成绩是( )A、95分 B、94分 C、84分 D、92分3. 在中,若 , , 则等于( )A、 B、 C、 D、4. 数据1, , 3,x,4有唯一的众数是3,则这组数据的中位数是( )A、 B、3 C、1 D、45. 四边形四边形 , , , . 则的度数是( )A、 B、 C、 D、6. 为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机取部分麦苗,获得苗高(单位;cm)的平均数与方差为: , ; , , 则麦苗又高又整齐的是( )A、甲 B、乙 C、丙 D、丁7. 已知一组数据, , , , 的平均数是2,方差是3.则另一组数据 , , , , 的平均数和方差分别是( )A、4,3 B、4,27 C、6,3 D、6,278. 一元二次方程的二次项,一次项和常数项分别为( )A、 , 无一次项, B、 , 无一次项,12 C、 , 0, D、 , 0,129. 用配方法解方程 , 配方后可得( )A、 B、 C、 D、10. 已知且 , , , 的最长边是10cm,则的面积是( )A、24 B、12 C、9 D、2011. 下列选项中,能使关于x的一元二次方程 , 一定有实数根的是( )A、 B、 C、 D、12. 某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程为( )A、 B、 C、 D、13. 如图,在△ABC中,DE∥BC, ,则下列结论中正确的是( )
 A、 B、 C、 D、14. 的结果是( )A、1 B、2 C、3 D、015. 若 , 则( )A、 B、4或 C、或2 D、416. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A、 B、 C、 D、14. 的结果是( )A、1 B、2 C、3 D、015. 若 , 则( )A、 B、4或 C、或2 D、416. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( ) A、
A、 B、
B、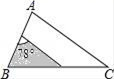 C、
C、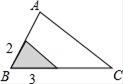 D、
D、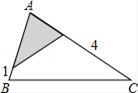
二、填空题(本大题有3小题,共9分。其中17题每空1分,18,19题每空3分)
-
17. 一组数据 , , , 0,1,2,3则这组数据的平均数是 , 中位数是 , 众数是18. 已知 , 是一元二次方程 的两实根,则 的值是 .19. 若 ( , , 均不为0),则 的值为
三、解答题(本大题共有7个小题,共72分)
-
20. 计算(1)、解方程:(用配方法)(2)、解方程:(用公式法)21. 如图,在平面直角坐标系中,点A、B的坐标分别为和 .
 (1)、以O为位似中心,在网格中作出的位似图形,使新图形与原图形的位似比为1:2.(2)、写出新图形各顶点的坐标.22. 如图,在中, , 垂足为D, , 分别交AB,AC,AD于点E,F,G, , , 求AG的长.
(1)、以O为位似中心,在网格中作出的位似图形,使新图形与原图形的位似比为1:2.(2)、写出新图形各顶点的坐标.22. 如图,在中, , 垂足为D, , 分别交AB,AC,AD于点E,F,G, , , 求AG的长. 23. 某工厂生产的一种产品按质量分为10个档次.若生产第一档次(最低档)的产品,则一天可以生产76件,每件的利润为10元.每提高一个档次,每件的利润增加2元,每天的产量将减少4件.设生产的产品质量的档次(每天只生产一个档次的产品)为x时,一天的利润为y元.(1)、用含x的代数式分别表示出每件产品的利润及每天生产的件数.(2)、若生产该产品一天的总利润为1080元,则该工厂生产的是第几档次的产品?24. 如图,某地政府为解决当地农户网络销售农特产品物流不畅问题,计划打通一条东西方向的隧道 .无人机从点A的正上方点C , 沿正东方向以 的速度飞行15s到达点D , 测得A的俯角为60°,然后以同样的速度沿正东方向又飞行50s到达点E , 测得点B的俯角为37°.
23. 某工厂生产的一种产品按质量分为10个档次.若生产第一档次(最低档)的产品,则一天可以生产76件,每件的利润为10元.每提高一个档次,每件的利润增加2元,每天的产量将减少4件.设生产的产品质量的档次(每天只生产一个档次的产品)为x时,一天的利润为y元.(1)、用含x的代数式分别表示出每件产品的利润及每天生产的件数.(2)、若生产该产品一天的总利润为1080元,则该工厂生产的是第几档次的产品?24. 如图,某地政府为解决当地农户网络销售农特产品物流不畅问题,计划打通一条东西方向的隧道 .无人机从点A的正上方点C , 沿正东方向以 的速度飞行15s到达点D , 测得A的俯角为60°,然后以同样的速度沿正东方向又飞行50s到达点E , 测得点B的俯角为37°.
(参考数据: , , , )
(1)、求无人机的高度 (结果保留根号);(2)、求 的长度(结果精确到1m).25. 某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了如表统计表及不完整的折线图.A,B产品单价变化统计表
第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
并求得了A产品三次单价的平均数和方差:
,
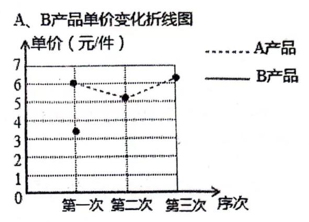 (1)、补全如图中B产品单价变化的折线图.B产品第三次的单价比上一次的单价降低了 ▲ %(2)、求B产品三次单价的方差,并比较哪种产品的单价波动小;(3)、该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调 , 使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.26. 如图,在中, , , . 动点P,Q分别从点B,C同时出发,点P以2cm/s的速度沿BC向点C移动,点Q以1cm/s的速度沿CA向点A移动.经过多少秒,以C,P,Q为顶点的三角形与相似?
(1)、补全如图中B产品单价变化的折线图.B产品第三次的单价比上一次的单价降低了 ▲ %(2)、求B产品三次单价的方差,并比较哪种产品的单价波动小;(3)、该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调 , 使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.26. 如图,在中, , , . 动点P,Q分别从点B,C同时出发,点P以2cm/s的速度沿BC向点C移动,点Q以1cm/s的速度沿CA向点A移动.经过多少秒,以C,P,Q为顶点的三角形与相似?