贵州省贵阳市2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-18 类型:期中考试
一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置作答,每小题3分,共36分.
-
1. 的结果是( )A、3 B、1 C、 D、2. 一元二次方程的二次项系数、一次项系数和常数项分别是( )A、1,2,1 B、1, , 1 C、0, , D、0, , 13. 如图,一条街道有两个拐角和 , 已知 , 若 , 则的度数是( )
 A、30° B、120° C、130° D、150°4. 小星参加学校举行的十佳歌手比赛,7位评委给他打分得到一组数据,为了比赛更加公平,这组数据要去掉一个最高分和一个最低分得到一组新数据,比较两组数据.一定不会发生变化的统计量是( )A、平均数 B、众数 C、中位数 D、方差5. 已知时,分式无意义,则□所表示的代数式是( )A、 B、 C、x D、2x6. 在一个不透明的口袋中装有5个红球和若干个白球,它们除颜色外其余均相同,通过多次摸球实验后发现,摸到红球的频率稳定在0.2附近,则估计口袋中的总球数大约是( )A、15 B、20 C、25 D、307. 已知 , 则以下对m的估算正确的是( )A、 B、 C、 D、8. 如图是一张横格数学作业纸,纸中的横线都平行,且相邻两条横线间的距离都相等.线段AC在横格纸上,与作业本的横格交于点B . 若 , 则AC的长是( )
A、30° B、120° C、130° D、150°4. 小星参加学校举行的十佳歌手比赛,7位评委给他打分得到一组数据,为了比赛更加公平,这组数据要去掉一个最高分和一个最低分得到一组新数据,比较两组数据.一定不会发生变化的统计量是( )A、平均数 B、众数 C、中位数 D、方差5. 已知时,分式无意义,则□所表示的代数式是( )A、 B、 C、x D、2x6. 在一个不透明的口袋中装有5个红球和若干个白球,它们除颜色外其余均相同,通过多次摸球实验后发现,摸到红球的频率稳定在0.2附近,则估计口袋中的总球数大约是( )A、15 B、20 C、25 D、307. 已知 , 则以下对m的估算正确的是( )A、 B、 C、 D、8. 如图是一张横格数学作业纸,纸中的横线都平行,且相邻两条横线间的距离都相等.线段AC在横格纸上,与作业本的横格交于点B . 若 , 则AC的长是( ) A、9 B、12 C、14 D、159. 如图,中 , 以B为圆心,任意长为半径作弧,分别交BC , BA于点F , G , 再分别以F , G为圆心,大于的长为半径作弧,两弧交于点H , 作射线BH , 交AD边于点E . 若 , 则的度数是( )
A、9 B、12 C、14 D、159. 如图,中 , 以B为圆心,任意长为半径作弧,分别交BC , BA于点F , G , 再分别以F , G为圆心,大于的长为半径作弧,两弧交于点H , 作射线BH , 交AD边于点E . 若 , 则的度数是( ) A、70° B、60° C、45° D、35°10. 若关于x的一元二次方程有两个不相等的实根,则m的值可以是( )A、0 B、 C、 D、11. 小红用四根相同长度的木条制作了一个四边形学具(如图①),测得其对角线AC的长为6cm, . 根据四边形的不稳定性,她将其变成了另一个四边形学具(如图②),使 , 则图②中对角线AC的长为( )
A、70° B、60° C、45° D、35°10. 若关于x的一元二次方程有两个不相等的实根,则m的值可以是( )A、0 B、 C、 D、11. 小红用四根相同长度的木条制作了一个四边形学具(如图①),测得其对角线AC的长为6cm, . 根据四边形的不稳定性,她将其变成了另一个四边形学具(如图②),使 , 则图②中对角线AC的长为( )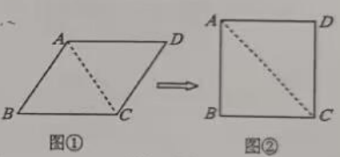 A、 B、 C、6 D、12. 三国时期的数学家赵爽在其所著的《勾股圆方图注》中记载过一元二次方程(正根)的几何解法,以方程即为例说明,记载的方法是:构造如下图,大正方形的面积是 . 同时它又等于四个矩形的面积加上中间小正方形的面积,即 , 因此 . 则在下面四个构图中(网格中每个小正方形边长为1个单位),能正确说明方程:解法的构图是( )
A、 B、 C、6 D、12. 三国时期的数学家赵爽在其所著的《勾股圆方图注》中记载过一元二次方程(正根)的几何解法,以方程即为例说明,记载的方法是:构造如下图,大正方形的面积是 . 同时它又等于四个矩形的面积加上中间小正方形的面积,即 , 因此 . 则在下面四个构图中(网格中每个小正方形边长为1个单位),能正确说明方程:解法的构图是( )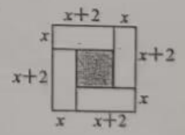 A、
A、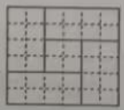 B、
B、 C、
C、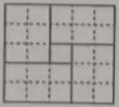 D、
D、
二、填空题:每小题4分,共16分.
-
13. 化简的结果是 .14. 2023年6月15日吉林一号高分06A系列卫星成功发射,创造了我国航天单次发射卫星数量最多的记录.发射前为确保万无一失,工程师对运载火箭的所有零部件进行了检查,则采用的调查方式是 . (填“普查”或“抽样调查”)15. 已知n是一元二次方程的根,代数式的值是 .16. 如图,在中, , D是AB的中点,过点D作BC的平行线,交AC于点E , 作BC的垂线,交BC于点F . 若 , 且的面积为 , 则BC的长是 .

三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
-
17. 计算:(1)、;(2)、 .18. 如图①,是两个长方体组合的几何体.
 (1)、图②和图③是它的两种视图,图②是视图,图③是视图;(填“主”“左”或“俯”)(2)、根据两个视图中的尺寸,计算这个组合几何体的体积.19. 随着信息技术的迅猛发展,移动支付已成为一种常见的支付方式.在一次购物中,小红和小星随机从“微信”“支付宝”“现金”三种支付方式中选一种方式进行支付(假设每种支付方式等可能且无关联).(1)、小红随机选择一种支付方式,选到“支付宝”支付的概率是;(2)、请用列表或画树状图法,求小红和小星恰好都选择“微信”支付的概率(依次记“微信”“支付宝”“现金”为A、B、C).20. 如图,中,D是边BC上的一点, .
(1)、图②和图③是它的两种视图,图②是视图,图③是视图;(填“主”“左”或“俯”)(2)、根据两个视图中的尺寸,计算这个组合几何体的体积.19. 随着信息技术的迅猛发展,移动支付已成为一种常见的支付方式.在一次购物中,小红和小星随机从“微信”“支付宝”“现金”三种支付方式中选一种方式进行支付(假设每种支付方式等可能且无关联).(1)、小红随机选择一种支付方式,选到“支付宝”支付的概率是;(2)、请用列表或画树状图法,求小红和小星恰好都选择“微信”支付的概率(依次记“微信”“支付宝”“现金”为A、B、C).20. 如图,中,D是边BC上的一点, . (1)、在BC上求作一点E , 使;(尺规作图,只保留作图痕迹,不要求写作法)(2)、求证: .21. 如图,直线与x轴,y轴分别相交于 , B两点.
(1)、在BC上求作一点E , 使;(尺规作图,只保留作图痕迹,不要求写作法)(2)、求证: .21. 如图,直线与x轴,y轴分别相交于 , B两点. (1)、b的值是 , 点B的坐标为;(2)、过B点的直线交x轴于点C , 且 , 求直线BC对应的函数表达式.22. 如图,在中, , 点D是AB的中点.
(1)、b的值是 , 点B的坐标为;(2)、过B点的直线交x轴于点C , 且 , 求直线BC对应的函数表达式.22. 如图,在中, , 点D是AB的中点.
求证: .
下面是两位同学两种添加辅助线的方法:

请选择一位同学的方法,完成证明.
23. 视力表对我们来说并不陌生,它蕴含着一定的数学知识.下面我们以标准对数视力表为例,来探索视力表中的奥秘.

用硬纸板复制视力表中所对应的“E”,并依次编号为①,②,放在水平桌面上.如图所示,将②号“E”沿水平桌面向右移动,直至从观测点O看去,对应顶点 , , O在一条直线上为止.这时我们说,在处用①号“E”测得的视力与在处用②号“E”测得的视力相同.
(1)、探究图中与之间的关系,请说明理由;(2)、若 , ①号“E”的测量距离 , 要使测得的视力相同,求②号“E”的测量距离 .24. 2023年杭州亚运会吉祥物组合名为“江南忆”,吉祥物一开售,就深受大家的喜爱.某商家销售吉祥物进价为15元,促销前销售单价为25元,平均每天能售出80件;根据市场调查,销售单价每降低1元,平均每天可多售出40件.(1)、若每件商品降价x元,则商店每天的平均销量是件(用含x的代数式表示);(2)、不考虑其他因素的影响,若商店平均每天至少要销售该商品200件,平均每天的利润达到1280元,每件商品的定价应为多少元?25. 小红在学习菱形的概念后,对菱形进一步开展探究活动:
如图①,在菱形ABCD中, , BD为对角线.
(1)、【问题解决】如图②,点E为BC延长线上一点,连接DE , 在线段DE上取点F使 , 点G为FB与CD的交点,则的度数是度;
(2)、【问题探究】如图③,点E为BC延长线上一点,连接DE , 在线段DE上取点F , 使 , 判断的形状,并说明理由;
(3)、【拓展延伸】如图③,在(2)的条件下,探究线段GC , CE , EF之间的数量关系,并说明理由.