贵州省六盘水市盘州市2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-18 类型:期中考试
一、选择题(每小题3分,共24分)
-
1. 若在实数范围内有意义,则x的取值范围是( )A、x≥1 B、x≤1 C、x>1 D、x≠12. 方程x2=2x的解是( )A、x=0 B、x=2 C、x1=0,x2=2 D、x1=0,x2=3. 如图,AD∥BE∥CF , 直线a、b与这三条平行线分别交于点A、B、C和点D、E、F , AB=4,BC=6,DE=3,则EF的长是( )
 A、4 B、5 C、6 D、4.54. 如图,在中, , 是斜边上的中线, , , 则的值是( )
A、4 B、5 C、6 D、4.54. 如图,在中, , 是斜边上的中线, , , 则的值是( ) A、 B、 C、 D、5. 如图,学校种植园是长32米,宽20米的距离.为便于管理,现要在中间开辟一横两纵三条等宽的小道,使种植面积为600平方米.若设小道的宽为米,则下面所列方程正确的是( )
A、 B、 C、 D、5. 如图,学校种植园是长32米,宽20米的距离.为便于管理,现要在中间开辟一横两纵三条等宽的小道,使种植面积为600平方米.若设小道的宽为米,则下面所列方程正确的是( ) A、 B、 C、 D、6. 已知点、在二次函数的图象上.若 , 则 与的大小关系是( )A、 B、 C、 D、7. 如图,在中,半径垂直弦于点D . 若 , 则的大小为( )
A、 B、 C、 D、6. 已知点、在二次函数的图象上.若 , 则 与的大小关系是( )A、 B、 C、 D、7. 如图,在中,半径垂直弦于点D . 若 , 则的大小为( ) A、 B、 C、 D、8.
A、 B、 C、 D、8.如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于( )
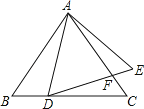 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(每小题3分,共18分)
-
9. 计算: =.10. 若关于的一元二次方程有实数根,则的取值范围是.11. 将抛物线向下平移2个单位后,得到的抛物线所对应的函数表达式为 .12. 如图,四边形ABCD内接于⊙O,E是BC延长线上一点,若∠BAD=105°,则∠DCE的度数是°.
 13. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则端点C的坐标为 .
13. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则端点C的坐标为 .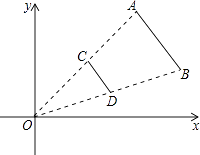 14. 如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B , 对称轴为直线 , 点C在抛物线上,且位于点A、B之间(C不与A、B重合).若四边形的周长为a , 则的周长为(用含a的代数式表示).
14. 如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B , 对称轴为直线 , 点C在抛物线上,且位于点A、B之间(C不与A、B重合).若四边形的周长为a , 则的周长为(用含a的代数式表示).
三、解答题(本大题共10小题,共78分)
-
15. 计算: .16. 解方程: .17. 某工厂一种产品2013年的产量是100万件,计划2015年产量达到121万件,假设2013年到2015年这种产品产量的年增长率相同,求2013年到2015年这种产品产量的年增长率.18. 图①、图②均是边长为1的正方形网格,的三个顶点都在格点上.按要求在图①、图②中各画一个三角形,使它的顶点均在格点上.
 (1)、在图①中画一个 , 满足 , 且相似比不为1:1.(2)、在图②中将绕点顺时针旋转得到 , 求旋转过程中点所经过的路径长.19. 如图,是半圆所在圆的直径,点O为圆心, , 弦 , 于E , 交于D , 连接、 .
(1)、在图①中画一个 , 满足 , 且相似比不为1:1.(2)、在图②中将绕点顺时针旋转得到 , 求旋转过程中点所经过的路径长.19. 如图,是半圆所在圆的直径,点O为圆心, , 弦 , 于E , 交于D , 连接、 . (1)、求的长.(2)、设 , 求的值.20. 如图,在平面直角坐标系中,过抛物线 的顶点A作x轴的平行线,交抛物线y=x2+1于点B , 点B在第一象限.
(1)、求的长.(2)、设 , 求的值.20. 如图,在平面直角坐标系中,过抛物线 的顶点A作x轴的平行线,交抛物线y=x2+1于点B , 点B在第一象限. (1)、求点A的坐标;(2)、点P为x轴上任意一点,连结AP、BP , 求△ABP的面积.21. 某超市利用一个带斜坡的平台装卸货物,其纵断面如图所示.为台面,垂直于地面,表示平台前方的斜坡.斜坡的坡角为 , 坡长为 . 为保障安全,又便于装卸货物,决定减小斜坡的坡角,是改造后的斜坡(在直线上),坡角为 . 求斜坡底端与平台的距离 . (结果精确到)【参考数据:;】
(1)、求点A的坐标;(2)、点P为x轴上任意一点,连结AP、BP , 求△ABP的面积.21. 某超市利用一个带斜坡的平台装卸货物,其纵断面如图所示.为台面,垂直于地面,表示平台前方的斜坡.斜坡的坡角为 , 坡长为 . 为保障安全,又便于装卸货物,决定减小斜坡的坡角,是改造后的斜坡(在直线上),坡角为 . 求斜坡底端与平台的距离 . (结果精确到)【参考数据:;】 22. 如图,在中, . 延长到O , 使 , 以O 为圆心,长为半径作交延长线于点D , 连结 .
22. 如图,在中, . 延长到O , 使 , 以O 为圆心,长为半径作交延长线于点D , 连结 . (1)、求扇形的面积.(2)、判断所在直线与的位置关系,并说明理由.23. 如图,在中, , , . 动点P从点B出发,在边上以每秒的速度向点A匀速运动,同时动点Q从点C出发, 在边上以每秒的速度向点B匀速运动,运动时间为t秒 .
(1)、求扇形的面积.(2)、判断所在直线与的位置关系,并说明理由.23. 如图,在中, , , . 动点P从点B出发,在边上以每秒的速度向点A匀速运动,同时动点Q从点C出发, 在边上以每秒的速度向点B匀速运动,运动时间为t秒 .
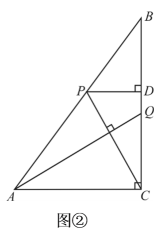 (1)、用含t的代数式表示的长.(2)、连结 , 如图①所示.当与相似时,求t的值.(3)、过点P作于D , 连结 , 如图②所示.当时,直接写出线段的长.24. 如图,在平面直角坐标系中,抛物线与x轴交于、两点,与y轴交于点C .
(1)、用含t的代数式表示的长.(2)、连结 , 如图①所示.当与相似时,求t的值.(3)、过点P作于D , 连结 , 如图②所示.当时,直接写出线段的长.24. 如图,在平面直角坐标系中,抛物线与x轴交于、两点,与y轴交于点C . (1)、求这条抛物线所对应的函数表达式.(2)、如图①,点D是x轴下方抛物线上的动点,且不与点C重合.设点D的横坐标为m , 以O、A、C、D为顶点的四边形面积为S , 求S与m之间的函数关系式.(3)、如图②,连结 , 点M为线段上一点,点N为线段上一点,且 , 直接写出当n为何值时为等腰三角形.
(1)、求这条抛物线所对应的函数表达式.(2)、如图①,点D是x轴下方抛物线上的动点,且不与点C重合.设点D的横坐标为m , 以O、A、C、D为顶点的四边形面积为S , 求S与m之间的函数关系式.(3)、如图②,连结 , 点M为线段上一点,点N为线段上一点,且 , 直接写出当n为何值时为等腰三角形.