贵州省铜仁市印江土家族苗族自治县2023-2024学年八年级上学期期中数学试题
试卷更新日期:2023-12-18 类型:期中考试
一、选择题(本题共12小题,每小题3分,共36分)
-
1. 在 , , , 中,是分式的有 ( )A、1个 B、2个 C、3个 D、4个2. 在日本核电站排放核废水期间,我国某监测点监测到极微量的人工放射性核素碘-131,其浓度为0.0000963贝克/立方米.数据“0.0000963”用科学记数法可表示为( )A、 B、 C、 D、3. 下列长度的三条线段,能组成三角形的是 ( )A、1、1、2 B、3、4、5 C、1、4、6 D、2、3、74. 下列语句中,是命题的个数为( )
①若两个角相等,则它们是对顶角;②等腰三角形两底角相等;③画线段;④同角的余角相等;⑤同位角相等.
A、2个 B、3个 C、4个 D、5个5. 如果把公式中的和都扩大了3倍,那么分式的值( )A、不变 B、扩大3倍 C、缩小3倍 D、缩小6倍6. 若分式 有意义,则a的取值范围是( )A、a=0 B、a="1" C、a≠﹣1 D、a≠07. 如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点P,若AB=5 cm,BC=3 cm,则△PBC的周长等于( )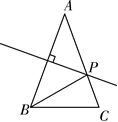 A、4 cm B、6 cm C、8 cm D、10 cm8. 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )
A、4 cm B、6 cm C、8 cm D、10 cm8. 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )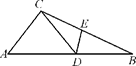 A、50° B、51° C、51.5° D、52.5°9. 若方程有增根,则增根可能为( )A、0 B、2 C、0或2 D、110. 若关于x的方程有解,则必须满足条件( )A、a≠b ,c≠d B、a≠b ,c≠-d C、a≠-b , c≠d D、a≠-b , c≠-d11.
A、50° B、51° C、51.5° D、52.5°9. 若方程有增根,则增根可能为( )A、0 B、2 C、0或2 D、110. 若关于x的方程有解,则必须满足条件( )A、a≠b ,c≠d B、a≠b ,c≠-d C、a≠-b , c≠d D、a≠-b , c≠-d11.如图所示的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=( )
 A、330° B、315° C、310° D、320°12. 如图,把纸片沿折叠,当点落在四边形内部时,与之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
A、330° B、315° C、310° D、320°12. 如图,把纸片沿折叠,当点落在四边形内部时,与之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )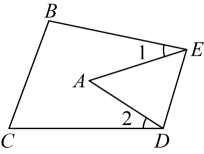 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题共4小题,每小题4分,共16分)
-
13. 当x= 时,分式的值为零.14. 等腰三角形的周长为20cm,一边长为6cm,则底边长为 cm.
15. 造房子时屋顶常用三角结构,从数学角度来看,是应用了 ;而活动挂架则用了四边形的 .16. 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①;②PQ//AE;③;④△CPQ为等边三角形;⑤;其中正确的有(注:把你认为正确的答案序号都写上)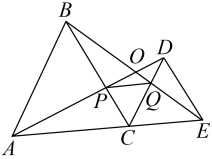
三、解答题(本题共8小题,共98分)
-
17. 计算:(1)、(2)、(3)、(4)、18. 化简: , 然后在不等式x≤2的非负整数解中选择一个适当的数代入求值.19. 解方程:(1)、(2)、20. 若关于x的方程无解,求 m 的值.21. 已知:如图,四边形中, , . 试说明: .
 22. 如图,在中, , , , 垂足为点 , , 垂足为点 , 图中与哪条线段相等?并说明理由.
22. 如图,在中, , , , 垂足为点 , , 垂足为点 , 图中与哪条线段相等?并说明理由.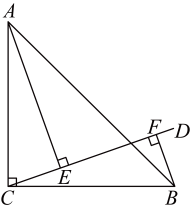 23. 书店老板去图书批发市场购买某种图书. 第一次用1200元购书若干本,并按该书定价7元出售,很快售完,由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了 , 他用1500元所购该书数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书. 试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?24. 感知:如图①所示,分别以的边 , 为边向外作等边、等边 , 连接 , . 易证:(不需要证明).
23. 书店老板去图书批发市场购买某种图书. 第一次用1200元购书若干本,并按该书定价7元出售,很快售完,由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了 , 他用1500元所购该书数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书. 试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?24. 感知:如图①所示,分别以的边 , 为边向外作等边、等边 , 连接 , . 易证:(不需要证明).探究:如图②所示,点是线段上方的一个动点,分别以的边 , 为直角边向外作等腰直角、等腰直角 , 且均以点为直角顶点,连接 , .
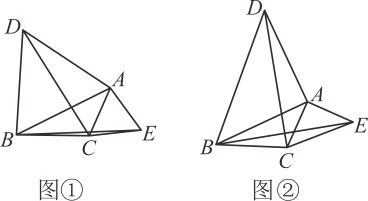 (1)、求证:;(2)、若 , , 则线段的最大值是 . (直接填答案,不需要过程)25. 如图所示,在等边中, , 点从点出发沿边向点以的速度移动,点从点出发沿边向点以的速度移动. , 两点同时出发,它们移动的时间为 .
(1)、求证:;(2)、若 , , 则线段的最大值是 . (直接填答案,不需要过程)25. 如图所示,在等边中, , 点从点出发沿边向点以的速度移动,点从点出发沿边向点以的速度移动. , 两点同时出发,它们移动的时间为 . (1)、请用表示和的长度.即 , .(2)、请问几秒钟后,为等边三角形?(3)、若 , 两点分别从 , 两点同时出发,并且能按顺时针方向沿三边运动,请问经过几秒钟后点与点在的哪条边上第一次相遇?
(1)、请用表示和的长度.即 , .(2)、请问几秒钟后,为等边三角形?(3)、若 , 两点分别从 , 两点同时出发,并且能按顺时针方向沿三边运动,请问经过几秒钟后点与点在的哪条边上第一次相遇?