河北省沧州市东光县2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-18 类型:期中考试
一、选择题(本大题共16个小题,共38分,1~6小题每小题3分,7~16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 下列图形为圆的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知一元二次方程的二次项系数为3,则一次项系数为( )A、 B、5 C、1 D、3. 平面内菱形和线段的位置如图所示(点 , 在点的正上方,),将线段绕点逆时针旋转,则下列菱形的顶点最可能在扫过范围内的是( )
2. 已知一元二次方程的二次项系数为3,则一次项系数为( )A、 B、5 C、1 D、3. 平面内菱形和线段的位置如图所示(点 , 在点的正上方,),将线段绕点逆时针旋转,则下列菱形的顶点最可能在扫过范围内的是( )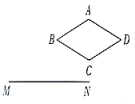 A、点 B、点 C、点 D、点4. 点关于原点中心对称的点的坐标为( )A、 B、 C、 D、5. 如图,若的直径为4,点到某条直线的距离为4,则这条直线可能是( )
A、点 B、点 C、点 D、点4. 点关于原点中心对称的点的坐标为( )A、 B、 C、 D、5. 如图,若的直径为4,点到某条直线的距离为4,则这条直线可能是( )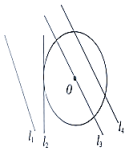 A、直线 B、直线 C、直线 D、直线6. 若 , 是抛物线上的两个点,则它的对称轴是( )A、 B、 C、 D、7. 三个全等的等边三角形按图1所示位置摆放,现添加一个大小相同的等边三角形,使四个等边三角形组成一个中心对称图形(如图2),则添加的等边三角形所放的位置是( )
A、直线 B、直线 C、直线 D、直线6. 若 , 是抛物线上的两个点,则它的对称轴是( )A、 B、 C、 D、7. 三个全等的等边三角形按图1所示位置摆放,现添加一个大小相同的等边三角形,使四个等边三角形组成一个中心对称图形(如图2),则添加的等边三角形所放的位置是( )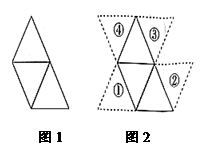 A、① B、② C、③ D、④8. 用开平方的方法解方程 , 做法正确的是( )A、 B、 C、 D、9. 如图,三角形乙是三角形甲经过旋转变换得到的,则说法正确的是( )
A、① B、② C、③ D、④8. 用开平方的方法解方程 , 做法正确的是( )A、 B、 C、 D、9. 如图,三角形乙是三角形甲经过旋转变换得到的,则说法正确的是( )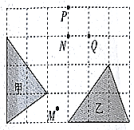 A、绕点逆时针旋转60° B、绕点顺时针旋转180° C、绕点逆时针旋转90° D、绕点顺时针旋转180°10. 二次函数的图象可能是( )A、
A、绕点逆时针旋转60° B、绕点顺时针旋转180° C、绕点逆时针旋转90° D、绕点顺时针旋转180°10. 二次函数的图象可能是( )A、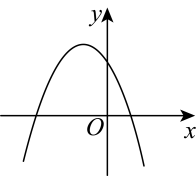 B、
B、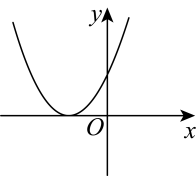 C、
C、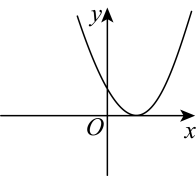 D、
D、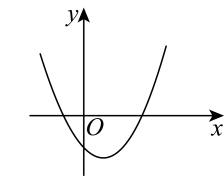 11. 如图,由图案(1)到图案(2)再到图案(3)的变化过程中,不可能用到的图形变换是( )
11. 如图,由图案(1)到图案(2)再到图案(3)的变化过程中,不可能用到的图形变换是( )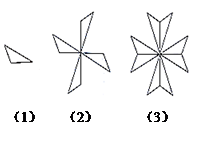 A、轴对称 B、旋转 C、中心对称 D、平移12. 如图,某大桥的桥拱可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面长度为300m,那么这些钢索中最长的一根为( )
A、轴对称 B、旋转 C、中心对称 D、平移12. 如图,某大桥的桥拱可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面长度为300m,那么这些钢索中最长的一根为( )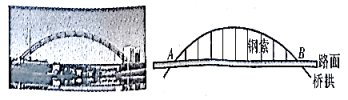 A、40m B、45m C、50m D、60m13. 老师设计了接力游戏,用合作的方式完成判断一元二次方程根的情况,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成判断.过程如图所示:
A、40m B、45m C、50m D、60m13. 老师设计了接力游戏,用合作的方式完成判断一元二次方程根的情况,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成判断.过程如图所示: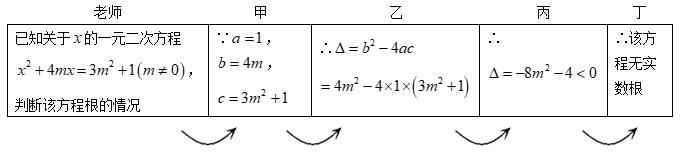
接力中,自己负责的一步出现错误的是( )
A、只有甲 B、甲和乙 C、乙和丙 D、乙和丁14. 如图,点在正六边形的对角线上,记图中6个三角形的面积分别为 , , , , , .若 , 则的值是( )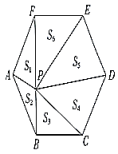 A、10 B、16 C、24 D、随点位置而变化15. 已知抛物线经过这两点与 , 若点在抛物线上,则可能的值是( )A、 B、 C、 D、16. 在黑板上有如下内容:“如图,是半圆所在圆的直径, , 点在半圆上,过点的直线交的延长线于点.”王老师要求添加条件后,编制一道题目.
A、10 B、16 C、24 D、随点位置而变化15. 已知抛物线经过这两点与 , 若点在抛物线上,则可能的值是( )A、 B、 C、 D、16. 在黑板上有如下内容:“如图,是半圆所在圆的直径, , 点在半圆上,过点的直线交的延长线于点.”王老师要求添加条件后,编制一道题目.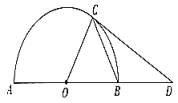
嘉嘉:若给出 , 则可证明直线是半圆的切线;
淇淇:若给出直线是的切线,且 , 则可求出的面积.
下列判断正确的是( )
A、嘉嘉和淇淇的都正确 B、只有淇淇的正确 C、嘉嘉和淇淇的都不正确 D、只有嘉嘉的正确二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分)
-
17. 若关于的一元二次方程有一个根的值是2,则的值是.18. 如图,在正方形中,已知点 , 点 ,
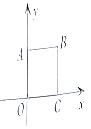
1 点B的坐标为.
2 当二次函数与正方形有公共点时,的最小值为.
19. 某西瓜经营户以2元/千克的价格购进一批西瓜,以3元/千克售出,每天可售出200千克,经调查,售价每降0.1元,每天多卖40千克,另外,每天的其它固定成本24元.当定价为元能获得最大利润,最大利润是元.三、解答题(本大题共七个小题,满分72分,解答题应写出必要的解题步骤或文字说明)
-
20. 如图所示,三角形和三角形关于某一点成中心对称,一同学不小心把墨水洒在了纸上,只能看到三角形和线段的对应线段 , 请你帮该同学找到对称中心 , 且补全三角形.
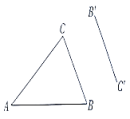 21. 如图,在平面直角坐标系中,、、是上的三个点,、、.
21. 如图,在平面直角坐标系中,、、是上的三个点,、、. (1)、圆心的坐标为;(2)、判断并说明点与的位置关系.22. 如图,已知的半径为 , 四边形内接于 , 连结、 , , .
(1)、圆心的坐标为;(2)、判断并说明点与的位置关系.22. 如图,已知的半径为 , 四边形内接于 , 连结、 , , .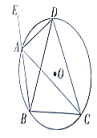 (1)、求的长;(2)、求证:平分的外角.23. 某西瓜地种植一种优质无籽西瓜,随着种植技术的不断改进,产量从2021的20t增加到2023年的28.8t.(1)、求这种无籽西瓜平均每年增产的百分率;(2)、若平均每年增产率不变,2025年该西瓜地的无籽西瓜产量能突破40t吗?24. 在平面直角坐标系中,抛物线(、为常数,)与轴交于和两点,与轴交于点.(1)、请用含的代数式表示;(2)、当时,
(1)、求的长;(2)、求证:平分的外角.23. 某西瓜地种植一种优质无籽西瓜,随着种植技术的不断改进,产量从2021的20t增加到2023年的28.8t.(1)、求这种无籽西瓜平均每年增产的百分率;(2)、若平均每年增产率不变,2025年该西瓜地的无籽西瓜产量能突破40t吗?24. 在平面直角坐标系中,抛物线(、为常数,)与轴交于和两点,与轴交于点.(1)、请用含的代数式表示;(2)、当时,①若抛物线的最小值为 , 求点的坐标;
②已知点在抛物线上,若 , 直接写出的取值范围;
25. 如图,在中, , 把绕点顺时针旋转,使点落到延长线上的点处,点落在点处,得到 , 旋转过程中得到两条弧和 , 与交于点 , 连接 , , .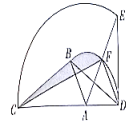 (1)、求的度数;(2)、若 , 求阴影部分的面积;(3)、若 , 与线段只有一个公共点 , 直接写出线段的取值范围.26. 如图,春节期间,某同学燃放一种手持烟花,烟花弹的飞行路径是一段抛物线,喷射出时距地面2米,在与他水平距离20米时,达到最大高度18米,这时烟花弹爆炸.若是哑弹(在空中没有爆炸的烟花弹),会继续按原有的抛物线飞落,在他的正前方33米处有一栋高15米的居民楼(其截面矩形与抛物线在同一平面上).
(1)、求的度数;(2)、若 , 求阴影部分的面积;(3)、若 , 与线段只有一个公共点 , 直接写出线段的取值范围.26. 如图,春节期间,某同学燃放一种手持烟花,烟花弹的飞行路径是一段抛物线,喷射出时距地面2米,在与他水平距离20米时,达到最大高度18米,这时烟花弹爆炸.若是哑弹(在空中没有爆炸的烟花弹),会继续按原有的抛物线飞落,在他的正前方33米处有一栋高15米的居民楼(其截面矩形与抛物线在同一平面上).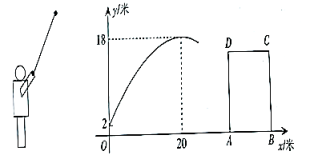 (1)、求抛物线的解析式(不必写出的取值范围),请通过计算说明若是哑弹,会落在几层居民楼的外墙或窗户上(每层楼高按3米计算);(2)、该同学沿轴负半轴至少后退几米,才能避免哑弹落在居民楼的外墙或窗户上?(3)、若居民楼宽 , 该同学沿轴向居民楼走米,可使哑弹落在楼顶上(不含点 , ),直接写出的取值范围.
(1)、求抛物线的解析式(不必写出的取值范围),请通过计算说明若是哑弹,会落在几层居民楼的外墙或窗户上(每层楼高按3米计算);(2)、该同学沿轴负半轴至少后退几米,才能避免哑弹落在居民楼的外墙或窗户上?(3)、若居民楼宽 , 该同学沿轴向居民楼走米,可使哑弹落在楼顶上(不含点 , ),直接写出的取值范围.【注:本题计算结果均不求近似值】