云南省普洱市思茅一中2022-2023学年七年级下学期开学考试试卷

试卷更新日期：2023-12-18 类型：开学考试

进入出卷网下载

一、单选题（共36分）

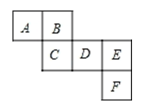
1. 如图，小明从上面观察一个圆柱体邮筒和一个正方体箱子，看到的是（　　）

A、 B、 C、 D、

查看试题解析
2. 中国共产主义青年团是中国青年的先锋队，是中国共产党的忠实助手和可靠后备军．截至2021年12月31日，全国共有共青团员7371.5万名，将7371.5万用科学记数法表示为（　　）

A、0.73715×10⁸ B、7.3715×10⁸ C、7.3715×10⁷ D、73.715×10⁶

查看试题解析
3. 设x，y，c是实数，正确的是（）

A、若x＝y，则x＋c＝y﹣c B、若x＝y，则xc＝yc C、若x＝y，则 $\frac{x}{c} = \frac{y}{c}$ D、若 $\frac{x}{2 c} = \frac{y}{3 c}$ ，则2x＝3y

查看试题解析
4. 用一个平面截一个正方体，截面形状不可能是（）

A、三角形 B、四边形 C、五边形 D、七边形

查看试题解析
5. 为积极响应我市创建“全国卫生城市”的号召，某校1500名学生参加了卫生知识竞赛，成绩记为A、B、C、D四等，从中随机抽取了部分学生成绩进行统计，绘制成如图两幅不完整的统计图表，根据图表信息，以下说法不正确的是（）

A、D等所在扇形的圆心角为15° B、样本容量是200 C、样本中C等所占百分比是10% D、估计全校学生成绩为A等大约有900人

查看试题解析
6. 下列等式，错误的是（　　）

A、5y³•3y⁵＝15y⁸ B、（﹣5a⁵b³c）÷（15a⁴b）＝﹣ $\frac{1}{3}$ ab²c C、（π﹣3）⁰＝1 D、（﹣xy）³＝﹣xy³

查看试题解析
7. 一个两位数，十位上的数比个位上的数的3倍大1，个位上的数与十位上的数的和等于9，这个两位数是（）

A、54 B、72 C、45 D、62

查看试题解析
8. 已知点M是线段AB上一点，若AM＝ $\frac{1}{4}$ AB ，点N是直线AB上的一动点，且AN﹣BN＝MN ，则 $\frac{M N}{A B}$ 的值（　　）

A、 $\frac{3}{4}$ B、 $\frac{1}{2}$ C、1或 $\frac{1}{2}$ D、 $\frac{3}{4}$ 或2

查看试题解析
9. 以下计算正确的是（　　）

A、（﹣2ab²）³＝8a³b⁶ B、3ab+2b＝5ab C、（﹣x²）•（﹣2x）³＝﹣8x⁵ D、2m（mn²﹣3m²）＝2m²n²﹣6m³

查看试题解析
10. 如图所示的是中国南宋数学家杨辉在详解《九章算法》中出现的三角形状的数列，又称为“杨辉三角形”该三角形中的数据排列有着一定的规律，若将其中一组斜数列用字母a₁、a₂ ， a₃ ， …代替，如图2，则a₉₉+a₁₀₀的值为（　　）

A、9801 B、10000 C、10201 D、10500

查看试题解析
11. 如图，A ， B两点在数轴上的位置表示的数分别为a ， b ．有下列四个结论：①（b﹣1）（a+1）＞0；② $\frac{b - 1}{| a - 3 |} > 0$ ；③（a+b）（a﹣b）＞0；④b＞﹣a＞﹣b＞a ．其中正确的结论是（　　）

A、①④ B、①② C、②③ D、②④

查看试题解析
12. 如图，点O为直线AB上一点，∠COD为直角，OE平分∠AOC ， OF平分∠COB ， OG平分∠BOD ．下列结论：
①∠FOG＝45°；②∠AOE+∠FOB＝90°；
③∠EOG＝130°；④∠AOC﹣∠BOD＝90°．
正确的有（　　）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题（共18分）

13. 如果|a+2|+（b﹣1）²＝0，那么代数式（a+b）²⁰²¹的值是．

查看试题解析
14. 某校开展捐书活动，七（1）班同学积极参与，现将捐书数量绘制成频数分布直方图（如图所示），如果捐书数量在3.5﹣4.5组别的人数占总人数的 $\frac{30}{100}$ ，那么捐书数量在4.5﹣5.5组别的人数是．

查看试题解析
15. 设a ， b ， c ， d为实数，现规定一种新的运算 $| \begin{array}{l} a c \\ b d \end{array} |$ ＝ad﹣bc ，则满足等式 $|\begin{matrix} \frac{x}{2} & \frac{x + 1}{3} \\ 2 & 1 \end{matrix}|$ ＝1的x的值为．

查看试题解析
16. 已知：A＝2x²+3xy﹣2x﹣1，B＝﹣x²+xy﹣1，若A+2B的值与x的取值无关，则y的值为．

查看试题解析
17. 直线l上的三个点A、B、C ，若满足BC＝ $\frac{1}{2}$ AB ，则称点C是点A关于点B的“半距点”．如图1，BC＝ $\frac{1}{2}$ AB ，此时点C就是点A关于点B的一个“半距点”．如图2若M、N、P三个点在同一条直线m上，且点P是点M关于点N的“半距点”，MN＝6cm ．则MP＝cm ．

查看试题解析
18. 已知n为奇数且a≠0，化简（8aⁿ⁺³﹣6aⁿ⁺²﹣5aⁿ⁺¹）÷（﹣a）ⁿ＝．

查看试题解析

三、解答题（共66分）

19. 如图，已知∠AOC＝ $\frac{1}{2}$ ∠BOC ， OD平分∠AOB ，且∠AOC＝40°．求∠COD ．

查看试题解析
20. 比较下列各组数的大小．

(1)、 $- 3 \frac{1}{2}$ 和 $- 2 \frac{1}{3}$ ；

(2)、﹣5和﹣|﹣4|；

(3)、 $- \frac{4}{5}$ 和 $- \frac{5}{4}$ ．

查看试题解析
21. 已知10^﹣2α＝3， $1 0^{- β} = \frac{1}{5}$ ，求10^6α+2β的值．

查看试题解析

22. 目前，全球淡水资源分布不均、总量不足是人类面临的共同问题，某市在实施居民用水定额管理前，通过简单随机抽样对居民生活用水情况进行了调查，获得了若干个家庭去年的月均用水量数据（单位：t），整理出了频数分布表，频数分布直方图和扇形统计图，部分信息如下：

月均用水量（t）	2≤x＜3.5	3.5≤x＜5	5≤x＜6.5	6.5≤x＜8	8≤x＜9.5
频数	7			6
对应的扇形区域	A	B	C	D	E

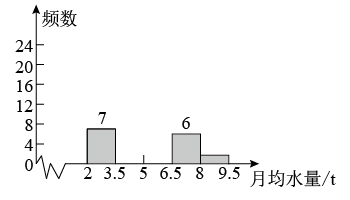
根据以上信息，解答下列问题：

(1)、补全频数分布直方图，并求出扇形图中扇形E对应的圆心角的度数；

(2)、为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5倍价格收费，若要使该市60％的家庭水费支出不受影响，你觉得家庭月均用水量应该定为多少？并说明理由．

查看试题解析

23. 小强的爸爸平常开车从家中到小强奶奶家，匀速行驶需要4小时，某天，他们以平常的速度行驶了 $\frac{1}{2}$ 的路程时遇到了暴雨，立即将车速减少了20千米／小时，到达奶奶家时共用了5小时，问小强家到他奶奶家的距离是多少千米？

查看试题解析
24. 如图，一只蚂蚁（点A表示）沿数轴向右爬了2个单位长度到达点B ，点A表示的数是 $- 1 \frac{1}{2}$ ，设点B所表示的数为m ．

(1)、求m的值；

(2)、若爬行到点C处时距离点B有1个单位长度，即BC＝1，求点C表示的数n的值；

(3)、在条件（1）、（2）下，求（m﹣1）²+|n+3 $\frac{1}{2}$ |的值．

查看试题解析
25. 一个三位数，它的个位数字是a ，十位数字是个位数字的3倍少1，百位数字比个位数字大5．

(1)、用a的式子表示此三位数；

(2)、若交换个位数字和百位数字，其余不变，则新得到的三位数字比原来的三位数减少了多少？

(3)、请你根据题目的条件思考，a的取值可能是多少？此时相应的三位数是多少？

查看试题解析
26. 如图是一个正方体的表面展开图，请回答下列问题：

(1)、与面B、C相对的面分别是；

(2)、若A＝a³+ $\frac{1}{5}$ a²b+3，B＝ $\frac{1}{2}$ a²b﹣3，C＝a³﹣1，D＝﹣ $\frac{1}{2}$ （a²b﹣6），且相对两个面所表示的代数式的和都相等，求E、F分别代表的代数式．

查看试题解析