重庆市荣昌名校校2024届高三上学期第二次月考数学试题

试卷更新日期：2023-12-18 类型：月考试卷

进入出卷网下载

一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中只有一项是符合题目要求的．

1. 已知集合 $A = {x | l n (x + 1) < 1} ， B = {y | y = e^{x} ， x \in R}$ ，则 $A ∩ B =$ （）

A、 $(- 1 ， e - 1)$ B、 $(0 ， e - 1)$ C、 $(1 ， e)$ D、 $(- 1 ， 0)$

查看试题解析
2. 已知复数 $z$ 满足 $z^{2} = 4 - 3 i$ ，则 $| z | =$ （）

A、5 B、 $\sqrt{5}$ C、13 D、 $\sqrt{13}$

查看试题解析
3. 已知p： $x + y > 0$ ， q： $l n (\sqrt{x^{2} + 1} + x) - l n (\sqrt{y^{2} + 1} - y) > 0$ ，则p是q的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 已知 $s i n (\frac{π}{4} - α) = \frac{3}{5}$ ，则 $\frac{s i n α}{1 - t a n α}$ 的值为（）

A、 $- \frac{7 \sqrt{2}}{60}$ B、 $\frac{7 \sqrt{2}}{60}$ C、 $- \frac{7 \sqrt{2}}{30}$ D、 $\frac{7 \sqrt{2}}{30}$

查看试题解析
5. 已知单位向量 $\vec{a} ， \vec{b} ， \vec{c}$ 满足 $\vec{a} + \vec{b} + \vec{c} = \vec{0}$ ，其中 $\vec{c} = (1 ， 0)$ ，则 $2 \vec{a} + \vec{b}$ 在 $\vec{c}$ 上的投影向量是（）

A、 $(- \frac{3}{2} ， - \frac{\sqrt{3}}{2})$ B、 $(\frac{3}{2} ， \frac{\sqrt{3}}{2})$ C、 $(\frac{3}{2} ， 0)$ D、 $(- \frac{3}{2} ， 0)$

查看试题解析
6. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，首项 $a_{1} = 1$ ，且满足 $a_{n + 1} + a_{n} = 3 \cdot 2^{n}$ ，则 $S_{11}$ 的值为（）

A、4093 B、4094 C、4095 D、4096

查看试题解析
7. 已知函数 $g (x) = \sqrt{3} \sin (ω x + φ)$ ， $g (x)$ 图像上每一点的横坐标缩短到原来的 $\frac{1}{2}$ ，得到 $f (x)$ 的图像， $f (x)$ 的部分图像如图所示，若 $\vec{A B} \cdot \vec{B C} = {| \vec{A B} |}^{2}$ ，则 $ω$ 等于（）

A、 $\frac{π}{12}$ B、 $\frac{π}{6}$ C、 $\frac{π}{4}$ D、 $\frac{π}{2}$

查看试题解析
8. 设 $a = \frac{2}{21} ， b = l n \frac{25}{21} ， c = s i n \frac{2}{21}$ ，则（）

A、 $a < b < c$ B、 $c < b < a$ C、 $c < a < b$ D、 $b < c < a$

查看试题解析

二、选择题：本大题共4小题，每小题5分，共20分在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．

9. 已知非零向量 $\vec{a} ， \vec{b} ， \vec{c}$ ，下列命题正确的是（）

A、若 $\vec{a} / / \vec{b} ， \vec{b} / / \vec{c}$ ，则 $\vec{a} / / \vec{c}$ B、与向量 $\vec{a}$ 共线的单位向量是 $\frac{\vec{a}}{| \vec{a} |}$ C、“ $\vec{a} \cdot \vec{b} > 0$ ”是“ $\vec{a}$ 与 $\vec{b}$ 的夹角是锐角”的充分不必要条件 D、若 $\vec{a} ， \vec{b}$ 是平面的一组基底，则 $\vec{a} + \vec{b} ， \vec{a} - \vec{b}$ 也能作为该平面的一组基底

查看试题解析
10. 设 $0 < a < b ， a + b = 1$ ，则下列结论正确的是（）

A、 $a^{2} + b^{2} > b$ B、 $a < 2 a b < \frac{1}{2}$ C、 $a > a^{2} + b^{2}$ D、 $\frac{1}{2} < a^{2} + b^{2} < 1$

查看试题解析
11. 设函数 $f (x) = \sqrt{3} s i n ω x c o s ω x - \frac{1}{2} c o s 2 ω x ， ω > 0 ，$ 则下列结论正确的是（）

A、 $\forall ω \in (0 ， 1) ， f (x)$ 在 $[- \frac{π}{6} ， \frac{π}{4}]$ 上单调递增； B、若 $ω = 1$ 且 $| f (x_{1}) - f (x_{2}) | = 2 ，$ 则 ${| x_{1} - x_{2} |}_{m i n} = π$ ； C、若 $| f (x) | = 1$ 在 $[0 ， π]$ 上有且仅有2个不同的解，则 $ω$ 的取值范围为 $ω \in [\frac{5}{6} ， \frac{7}{3})$ ； D、存在 $ω \in (0 ， 1)$ ，使得 $f (x)$ 的图象向左平移 $\frac{π}{6}$ 个单位长度后得到函数 $g (x)$ 为奇函数.

查看试题解析
12. 如图，在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，E是线段 $A D_{1}$ 的中点，点M，N满足 $\vec{A_{1} M} = λ \vec{A_{1} C} ， \vec{B_{1} N} = μ \vec{B_{1} C_{1}}$ ，其中 $λ ， μ \in (0 ， 1)$ ，则（）

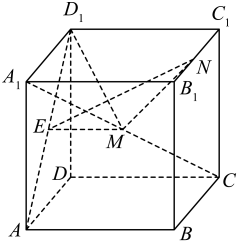A、存在 $λ ， μ \in (0 ， 1)$ ，使得 $E M ⊥ E N$ B、 $M N$ 的最小值为 $\sqrt{2}$ C、当 $λ = \frac{1}{2} ， μ = \frac{3}{4}$ 时，直线 $D_{1} M$ 与平面 $M E N$ 所成角的正弦值为 $\frac{\sqrt{15}}{15}$ D、当 $λ = \frac{1}{2} ， μ = \frac{2}{3}$ 时，过E，M，N三点的平面截正方体得到的截面多边形面积为 $\frac{4 \sqrt{10}}{3}$

查看试题解析

三、填空题：本大题共4小题，每小题5分，共20分．

13. 已知一个圆锥的侧面积为 $6 π$ ，它的侧面展开图是一个半圆，则此圆锥的体积为.

查看试题解析
14. 已知 $s i n (α + \frac{π}{5}) = \frac{2}{5}$ ，则 $s i n (2 α - \frac{π}{10}) =$ .

查看试题解析
15. 设函数 $f (x) = e^{x} + e^{- x} - \frac{1}{l g (x^{2} + 1)}$ ，则使得 $f (2 x + 1) < f (x - 2)$ 成立的 $x$ 的取值范围是.

查看试题解析
16. 在等腰梯形 $A B C D$ 中， $A B = 2 C D = 2$ ， $∠ D A B = ∠ C B A = \frac{π}{3}$ ， $O$ 为 $A B$ 的中点.将 $△ B O C$ 沿 $O C$ 折起，使点 $B$ 到达点 $B^{'}$ 的位置，则三棱锥 $B^{'} - A D C$ 外接球的表面积为；当 $B^{'} D = \frac{\sqrt{3}}{2}$ 时，三棱锥 $B^{'} - A D C$ 外接球的球心到平面 $B^{'} C D$ 的距离为.

查看试题解析

四、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．

17. 已知等差数列 ${a_{n}}$ 满足 $a_{6} + a_{7} = 4$ ，且 $a_{1} ， a_{4} ， a_{5}$ 成等比数列．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、记 $T_{n}$ 为数列 ${a_{n}}$ 前 $n$ 项乘积，若 $a_{1} < 0$ ，求 $T_{n}$ 的最大值．

查看试题解析
18. $f (x) = s i n x c o s (x + \frac{π}{3}) - s i n (x + \frac{π}{2}) s i n (x - \frac{2 π}{3})$

(1)、求函数 $f (x)$ 的中心对称点；

(2)、先将函数 $y = f (x)$ 的图象上的点的横坐标缩小到原来的 $\frac{1}{2}$ ，纵坐标保持不变，再把所得的图象向右平移 $\frac{π}{6}$ 个单位，得到函数 $y = g (x)$ ，解关于 $x$ 的不等式 $g (x) < f (- \frac{π}{3})$ .

查看试题解析
19. 如图， $△ A B C$ 为正三角形， $A E ⊥$ 平面 $A B C ， C D ⊥$ 平面 $A B C ， A C = C D ， A E = 2 C D$ ，点 $F ， P$ 分别为 $A B ， B D$ 的中点，点 $Q$ 在线段 $B E$ 上，且 $B E = 4 B Q$ ．

(1)、证明：直线 $C P$ 与直线 $F Q$ 相交；

(2)、求平面 $C P F$ 与平面 $B D E$ 夹角的余弦值．

查看试题解析
20. 2023年9月8日，第19届亚运会火炬传递启动仪式在杭州西湖景区涌金公园广场成功举行．火炬传递首日传递从杭州西湖涌金公园广场出发，沿南山路—湖滨路—环城西路—北山街—西泠桥—孤山路传递，在“西湖十景”之一的平湖秋月收火．杭州亚运会火炬首日传递共有106棒火炬手参与．

(1)、组委会从全省火炬手中随机抽取了100名火炬手进行信息分析，得到如下表格：
性别
年龄
总计
满50周岁
未满50周岁
男
15
45
60
女
5
35
40
总计
20
80
100
$α$
0.1
0.05
0.01
0.005
0.001
$x_{α}$
2.706
3.841
6.635
7.879
10.828
根据小概率值 $α = 0.1$ 的 $χ^{2}$ 独立性检验，试判断全省火炬手的性别与年龄满或未满50周岁是否有关联；

(2)、在全省的火炬手中，男性占比72%，女性占比28%，且50%的男性火炬手和25%的女性火炬手喜欢观看足球比赛．某电视台随机选取一位喜欢足球比赛的火炬手做访谈，请问这位火炬手是男性的概率为多少？

查看试题解析
21. 在 $△ A B C$ 中，角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ 且 $b c o s C + c s i n B = a ， \frac{a + 2 b}{s i n A + 2 s i n B} = 6 \sqrt{2}$ ，

(1)、求 $b$ ；

(2)、求 $A C$ 边上中线长的取值范围．

查看试题解析
22. 设函数 $f (x) = - 3 l n x + x^{3} + a x^{2} - 2 a x ， a \in R$ .

(1)、求函数 $f (x)$ 在 $x = 1$ 处的切线方程；

(2)、若 $x_{1} ， x_{2}$ 为函数 $f (x)$ 的两个不等于1的极值点，设 $P (x_{1} ， f (x_{1})) ， Q (x_{2} ， f (x_{2}))$ ，记直线 $P Q$ 的斜率为 $k$ ，求证： $k + 2 < x_{1} + x_{2}$ .

查看试题解析

性别		年龄					总计
		满50周岁			未满50周岁
男		15			45		60
女		5			35		40
总计		20			80		100
$α$	0.1		0.05	0.01		0.005		0.001
$x_{α}$	2.706		3.841	6.635		7.879		10.828