人教版（贵州地区）初中数学2023-2024学年七年级上学期期末模拟卷（三）

试卷更新日期：2023-12-17 类型：期末考试

进入出卷网下载

一、选择题

1. 下列各数-1，2，-3，0，-2中，负数的个数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列各组数中，互为倒数的是（）

A、-0.125与 $\frac{1}{8}$ B、-0.5与2 C、-1与2 D、 $- 1 \frac{1}{4}$ 与 $- \frac{4}{5}$

查看试题解析
3. 作为世界文化遗产的长城，其总长大约为6 700 000m，将6 700 000用科学记数法表示为（）

A、670×10⁴ B、67×10⁵ C、6.7×10⁶ D、0.67×10⁷

查看试题解析
4. 下列各式中，变形正确的是（）

A、若 $a = b$ ，则 $a + c = b + c$ B、若 $2 x = a$ ，则 $x = a - 2$ C、若 $6 a = 2 b$ ，则 $a = 3 b$ D、若 $a = b + 2$ ，则 $3 a = 3 b + 2$

查看试题解析
5. 下列方程中是一元一次方程的是（）

A、 $\frac{x}{3} - 3 = 4 + \frac{x}{4}$ B、 $2 x + 3 x - 1$ C、 $x^{2} - 3 x + 3 = 0$ D、 $x + 2 y = 3$

查看试题解析
6. 用一个平面去截一个几何体，不能截得三角形截面的几何体是（）

A、圆柱 B、圆锥 C、三棱柱 D、正方体

查看试题解析
7. 下列计算正确的是（）

A、 $\frac{1}{3} - \frac{1}{3}$ ×4=0×4=0 B、4÷（-2）×（ $- \frac{1}{2}$ ）=4÷1=4 C、-3²-（-2）³=9-8=1 D、 $(- \frac{1}{4}) \div (\frac{1}{12} + \frac{1}{16}) = (- \frac{1}{4}) \div \frac{7}{48} = - \frac{12}{7}$

查看试题解析
8. 下列说法正确的是（　　）

A、a²+2a+3²是三次三项式 B、 $\frac{x y^{2}}{4}$ 的系数是4 C、 $\frac{x - 3}{2}$ 的常数项是﹣3 D、0是单项式

查看试题解析
9. 实数a ， b ， c在数轴上的对应点的位置如图所示，若|a|＝|b|，则下列结论中错误的是（）

A、a+b＝0 B、a+c＜0 C、b+c＞0 D、ac＜0

查看试题解析
10. 把方程 $\frac{3 x}{0.2}$ ﹣1＝ $\frac{2 x}{0.3}$ 的分母化为整数可得方程（）

A、 $\frac{30 x}{2}$ ﹣10＝ $\frac{20 x}{3}$ B、 $\frac{30 x}{2}$ ﹣1＝ $\frac{20 x}{3}$ C、 $\frac{30 x}{2}$ ﹣10＝ $\frac{2 x}{3}$ D、 $\frac{3 x}{2}$ ﹣1＝ $\frac{2 x}{3}$

查看试题解析
11. 整理一批图书，由一个人做要30小时完成，现计划由一部分人先做3小时，然后增加2人与他们一起做6小时，完成这项工作，假设这些人的工作效率相同，具体应先安排多少人工作？如果设安排x人先做3小时，下列四个方程中正确的是（）

A、 $\frac{3 x}{30} + \frac{6 (x + 2)}{30} = 1$ B、 $\frac{3 (x + 2)}{30} + \frac{6 x}{30} = 1$ C、 $\frac{3 x}{30} + \frac{6 (x - 2)}{30} = 1$ D、 $\frac{3 x}{30} + \frac{6 x}{30} = 1$

查看试题解析
12. 把夏禹时代的“洛书”用数学符号翻译出来就是一个三阶幻方，它的每行.每列.每条对角线上三个数之和均相等，那么幻方中 $a$ 的值是（）

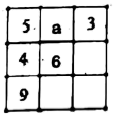A、6 B、8 C、10 D、12

查看试题解析

二、填空题

13. $| - \frac{1}{3} |$ 的相反数是.

查看试题解析
14. 计算：36°55′＋32°15′＝．

查看试题解析
15. 若方程(a-2)x^|a|-1+3=0是关于x的一元一次方程，则a=

查看试题解析
16. 如图，按下列程序进行计算，经过三次输入，最后输出的数是12，则最初输入的数是 .

查看试题解析
17. 如图，长度为12cm的线段AB的中点是点M，点C在线段MB上，且 $M C ： C B = 1 ： 2$ ，则线段AC的长为．

查看试题解析

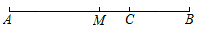
三、计算题

18. 计算：

(1)、（-15）+（+7）-（-3）．

(2)、4+（-2）²×2-（-36）÷4

查看试题解析
19. 解方程： $4 - 3 (10 - y) = 5 y$ ．

查看试题解析
20. 解方程： $\frac{1 + x}{0.1} - \frac{0.4 x - 0.5}{0.2} = \frac{1}{2}$

查看试题解析

四、作图题

21. 画图题

(1)、如图，已知三点A、B、C.

①画直线 $A B$ ；

②射线 $A C$ ；

③线段 $B C$ ；

④在线段 $B C$ 上取点D；

⑤延长 $B C$ 到E，使 $C E = C D$ .

(2)、将下列各数在数轴上表示出来，并把它们用“>”连接起来.
$- 1$ ，2，3， $- 2.5$ .

查看试题解析

五、解答题

22. 先化简，再求值：2xy-3（x²y-xy²）+ 2（x²y-xy²-xy），其中x为最小的正整数，y为最大的负整数．

查看试题解析
23. 如图，已知直线CD、EF相交于点O，OA⊥OB，且OC平分∠AOF，∠BOE=2∠AOE，求∠BOD的大小.

查看试题解析
24. 为扎实推进“精准扶贫”工作，某“贫困户”在党和政府的关怀和帮助下投资了一个鱼塘，经过一年多的精心养殖，今年10月份从鱼塘里捕捞了草鱼和花鲢鱼共2500千克，在市场上草鱼以每千克16元的价格出售，花鲢鱼以每千克24元的价格出售，这样该贫困户10月份收入52000元．

(1)、今年10月份从鱼塘里捕捞草鱼和花鲢鱼各多少千克？

(2)、该贫图户今年12月份再次从鱼塘里捕捞．在捕捞数量和销售价格方面，草鱼数量比10月份减少了 $6 a$ 千克，销售价格不变；花鲢鱼数量比10月份成少了 $a %$ ，销售价格比10月份减少了 $\frac{1}{6}$ ，该贫困户在10月份和12月份两次捕捞中共收入了94040元，真正实现了脱贫致富，试求a的值．

查看试题解析
25. 某文艺团体为“希望工程”募捐义演，全价票为每张18元，学生享受半价，某场演出共售出966张票，收入15480元，问这场演出共售出学生票多少张.

查看试题解析
26. 数轴上 $A$ ， $B$ 两个点对应的数分别是 $a$ ， $b$ ，一般地，把 $| a - b |$ 称为点 $A$ 与点 $B$ 之间的距离，并记作 $A B$ ．
如图：数轴上 $A$ ， $B$ 两个点对应的数分别是 $a$ ， $b$ ，且 $| a + 3 | + (b - 6)^{2} = 0$ ．

(1)、求 $A B$ ．

(2)、点 $M$ 为数轴上一点，当 $M A = M B$ 时，求点 $M$ 所对应的数．

(3)、直接写出点 $M$ 对应的数为多少时， $M A = 2 M B$ ．

查看试题解析

六、实践探究题

27. 阅读下列材料：
我们规定：若关于 $x$ 的一元一次方程 $a x = b$ 的解为 $x = b + a$ ，则称该方程为“和解方程”.例如：方程 $2 x = - 4$ 的解为 $x = - 2$ ，而 $- 2 = - 4 + 2$ ，则方程 $2 x = - 4$ 为“和解方程”.请根据上述规定解答下列问题：

(1)、下列关于 $x$ 的一元一次方程是“和解方程”的有：.
① $\frac{2}{3} x = - \frac{2}{3}$ ；② $- 3 x = \frac{9}{4}$ ；③ $5 x = - 2$

(2)、若关于 $x$ 的一元一次方程 $3 x = 2 a - 10$ 是“和解方程”，求 $a$ 的值.

查看试题解析