人教版（贵州地区）初中数学2023-2024学年七年级上学期期末模拟卷（二）

试卷更新日期：2023-12-17 类型：期末考试

进入出卷网下载

一、选择题

1. 若规定收入为“ $+$ ”，那么 $- 50$ 元表示（　　）

A、收入了 $50$ 元 B、支出了 $50$ 元 C、没有收入也没有支出 D、收入了 $100$ 元

查看试题解析
2. 长春轨道客车股份有限公司制造的新型奥运版复兴号智能动车组，车头采用鹰隼形的设讨，能让性能大幅提升，一列该动车组一年运行下来可节省约1800000度电，将数据1800000用科学记数法表示为（）

A、18×10⁵ B、1.8×10⁶ C、1.8×10⁷ D、0.18×10⁷

查看试题解析
3. 下列方程中，是一元一次方程的是（）

A、 $3 x - 2 y = 1$ B、 $1 + \frac{1}{x} = x$ C、 $x^{2} = 9$ D、 $2 x - 1 = 3$

查看试题解析
4. 小王准备从 $A$ 地到 $B$ 地，打开导航，显示两地的距离为 $10.6 km$ ，但导航提供的三条可选路线长却分别为 $13 km$ ， $14 km$ ， $17 km$ （如图），下列解释这一现象的数学知识最合理的是（）

A、两点之间，线段最短 B、两点之间，直线最短 C、垂线段最短 D、两点确定一条直线

查看试题解析
5. 下列各式运算正确的是（）

A、2（a-1）=2a-1 B、a²b-ab²=0 C、a⁵+a⁵=2a⁵ D、2a³-3a³=a³

查看试题解析
6. 实数a，b在数轴上对应点的位置如图所示，下列结论正确的是（）

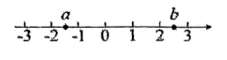A、a>0 B、a<b C、b-1<0 D、ab>0

查看试题解析
7. 下列方程变形中，正确的是（）

A、方程 $\frac{x - 1}{2} - \frac{x}{5} = 1$ ，去分母得 $5 (x - 1) - 2 x = 10$ B、方程 $3 - x = 2 - 5 (x - 1)$ ，去括号得 $3 - x = 2 - 5 x - 1$ C、方程 $\frac{2}{3} t = \frac{3}{2}$ ，系数化为 $1$ 得 $t = 1$ D、方程 $3 x - 2 = 2 x + 1$ ，移项得 $3 x - 2 x = - 1 + 2$

查看试题解析
8. 若 $- x^{3} y^{m}$ 与 $y x^{n}$ 是同类项，则 $m + 2 n$ 的值为（）

A、7 B、5 C、3 D、2

查看试题解析
9. 《九章算术》是中国传统数学最重要的著作之一.书中记载：“今有人共买鸡，人出九，盈十一；人出六，不足十六.问人数几何？”意思是：“有若干人共同出钱买鸡，如果每人出九钱，那么多了十一钱；如果每人出六钱，那么少了十六钱.问：共有几个人？”设共有 $x$ 个人共同出钱买鸡，则下面所列方程正确的是（）.

A、 $9 x + 11 = 6 x - 16$ B、 $9 x - 11 = 6 x + 16$ C、 $6 x - 11 = 9 x + 16$ D、 $6 x + 11 = 9 x - 16$

查看试题解析
10. 一列数，按一定规律排列成： $- 1, 2, - 4, 8, - 16$ ，…，从中取出三个相邻的数，若三个数的和为a，则这三个数中最大数与最小数的差为（）

A、a B、 $| a |$ C、 $2 | a |$ D、 $2 a$

查看试题解析
11. 数据8.641按四舍五人精确到0.01的结果是（）

A、8.6 B、9.0 C、8.65 D、8.64

查看试题解析
12. 下列计算正确的是（　　）

A、0-（-5）＝-5 B、-2÷ $\frac{1}{3}$ ×3＝-2 C、（- $\frac{1}{5}$ ）÷5＝-1 D、（-3）+（-9）＝-12

查看试题解析

二、填空题

13. 比较大小： $- \frac{5}{6}$ $- \frac{7}{8}$

查看试题解析
14. 若∠1=75°，则∠1的补角的大小为

查看试题解析
15. 如果 $- 6 x^{5 m - 9} + 8 = 0$ 是关于 $x$ 的一元一次方程，那么 $m =$ ．

查看试题解析
16. 一项工程，甲队单独完成需要12天，乙队单独完成需要24天，现在由甲、乙两队共同工作3天后甲队另有任务离开，剩下的工程由乙队完成，求完成这项工程所用的时间．若设完成此项工程共用x天，则可列得方程是．

查看试题解析
17. 如图，点C为线段 $A B$ 上一点，若线段 $A C = 12 c m$ ， $A C ： C B = 3 ： 2$ ， D，E两点分别为 $A C$ ， $A B$ 的中点，则 $D E$ 的长为 $c m$ ．

查看试题解析

三、计算题

18. 有理数的混合运算

(1)、 ${(- 2)}^{3} \div 4 \times [5 - {(- 3)}^{2}]$ ；

(2)、 $(\frac{1}{2} + \frac{5}{6} - \frac{7}{12}) \times (- 24)$

查看试题解析
19. 解方程：

(1)、3-(5-2x)=x+2．

(2)、 $\frac{x + 2}{2} - \frac{2 x + 3}{3}$ =1

查看试题解析

四、解答题

20. 已知A，B，C三点在数轴上如图所示，它们表示的数分别是a ， b，c.且|a|<|b|.

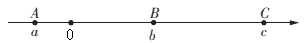(1)、填空：abc0，a+b0（填“>”“<”或“=”）.

(2)、化简：|a-b|-2|a+b|+|b-c|.

查看试题解析
21. 已知： $A = 2 a^{2} - 3 a b - 5 a - 1$ ， $B = - a^{2} + a b - 1$ ．

(1)、求 $3 A + 6 B$ ；

(2)、若 $3 A + 6 B$ 的值与a的取值无关，求b的值．

查看试题解析
22. （总量相等问题）某校春游，若包租相同的大巴13辆，那么就有14人没有座位；如果多包租1辆，那么就多了26个空位，问春游的总人数是多少？

查看试题解析
23. 植树节，某校植树任务为n棵树苗，九年级共种了任务数的一半，八年级种了剩下任务数的一半，七年级种完了剩下的所有树苗．

(1)、用关于n的代数式分别表示每个年级所种的树苗数．

(2)、若七年级种的树苗数为30棵，问全校的植树任务是多少棵？

查看试题解析
24. 数轴上 $A$ ， $B$ 两个点对应的数分别是 $a$ ， $b$ ，一般地，把 $| a - b |$ 称为点 $A$ 与点 $B$ 之间的距离，并记作 $A B$ ．
如图：数轴上 $A$ ， $B$ 两个点对应的数分别是 $a$ ， $b$ ，且 $| a + 3 | + (b - 6)^{2} = 0$ ．

(1)、求 $A B$ ．

(2)、点 $M$ 为数轴上一点，当 $M A = M B$ 时，求点 $M$ 所对应的数．

(3)、直接写出点 $M$ 对应的数为多少时， $M A = 2 M B$ ．

查看试题解析
25. A、B、C、D四个车站的位置如图所示，求：

(1)、A、D两站的距离；

(2)、A、C两站的距离．

查看试题解析
26. 如果A、B两点在数轴上分别表示有理数a、b ，那么它们之间的距离 $A B = | a - b |$ ．如图1，已知数轴上两点A、B对应的数分别为－3和8，数轴上另有一个点P对应的数为x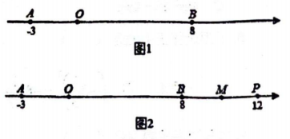

(1)、点P、B之间的距离 $P B =$ ．

(2)、若点P在A、B之间，则 $| x + 3 | + | x - 8 | =$ ．

(3)、①如图2，若点P在点B右侧，且 $x = 12$ ，取BP的中点M ，试求2AM－AP的值．
②若点P为点B右侧的一个动点，取BP的中点M ，那么2AM－AP是定值吗？如果是，请求出这个定值；如果不是，请说明理由．

查看试题解析

五、实践探究题

27. 我们知道， $| a |$ 可以理解为 $| a - 0 |$ ，它表示：数轴上表示数 $a$ 的点到原点的距离，这是绝对值的几何意义．进一步地，数轴上的两个点 $A$ ， $B$ ，分别用数 $a$ ， $b$ 表示，那么 $A$ ， $B$ 两点之间的距离为 $A B = | a - b |$ ，反过来，式子 $| a - b |$ 的几何意义是：数轴上表示数 $a$ 的点和表示数 $b$ 的点之间的距离．利用此结论，回答以下问题：

(1)、数轴上表示数 $- 5$ 的点和表示数 $3$ 的点之间的距离是；

(2)、数轴上点 $A$ 用数 $a$ 表示，若 $| a | = 5$ ，那么 $a$ 的值为；

(3)、数轴上点 $A$ 用数 $a$ 表示，探究以下几个问题：
$①$ 若 $| a - 3 | = 5$ ，那么 $a$ 的值是    ▲        ；
$②$ 满足 $| a + 2 | + | a - 3 | = 5$ 整数 $a$ 有    ▲        个；
$③ | a - 3 | + | a + 2022 | |$ 有最小值，最小值是：    ▲        ；
$④$ 求 $| a + 1 | + | a + 2 | + | a + 3 + \dots \dots | a + 2021 + | a + 2022 | + | a + 2023 |$ 的最小值．

查看试题解析