湖北省武汉市黄陂区2023-2024学年七年级上学期数学期中试卷

试卷更新日期：2023-12-16 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分）本题共10小题，每小题均给出A，B，C，D四个选项，有且只有一个答案是正确的，请将正确答案的代号填在答题卡上，填在试题卷上无效．

1. 我国古代数学著作《九章算术》中首次正式引入负数，如果支出200元记作 $- 200$ 元，那么收入60元记作（　　）

A、 $- 60$ 元 B、 $+ 60$ 元 C、140元 D、 $- 140$ 元

查看试题解析
2. 在 $45 %$ ， $- (- 5)$ ， 0， $- (+ 2)$ 这四个数中，负数是（）

A、 $45 %$ B、 $- (- 5)$ C、0 D、 $- (+ 2)$

查看试题解析
3. 2023年中秋国庆“双节”期间，大美黄陂以丰富多元的文旅产品吸引八方来客，各大景区景点游客量迎来井喷式增长．全区共接待游客约193万人次，用科学记数法表示数据193万为（）

A、 $19.3 \times 1 0^{5}$ B、 $1.93 \times 1 0^{6}$ C、 $0.193 \times 1 0^{7}$ D、 $1.93 \times 1 0^{8}$

查看试题解析
4. 下列计算或化简正确的是（）

A、 $5 a^{2} - 2 a = 3 a$ B、 $a + 2 b = 3 a b$ C、 $4 a^{2} b - b a^{2} = 3 a^{2} b$ D、 $a - (b - c) = a - b - c$

查看试题解析
5. 下列关系式不成立的是（）

A、 $\frac{- a}{b} = \frac{a}{- b} = - \frac{a}{b}$ B、 $\frac{- a}{- b} = \frac{a}{b}$ C、若 $a < 0$ ， $b < 0$ ，则 $\frac{a b}{a + b} < 0$ D、若 $a < b$ ， $\frac{b}{a} < 0$ ，则 $a > 0$

查看试题解析
6. 单项式 $m x y^{3}$ 与 $x^{n + 2} y^{3}$ 的和是 $5 x y^{3}$ ，则 $m - n ($ （）

A、-4 B、3 C、4 D、5

查看试题解析
7. 已知数a ， b在数轴上， $| a + 1 | = 4$ ， b比最大的负整数大2，则 $a - b$ 的值是（）

A、2 B、 $- 4$ C、2或 $- 6$ D、2或 $- 4$

查看试题解析
8. 某商店在甲批发市场以每包 $a$ 元的价格购进 $35$ 包茶叶，又在乙批发市场以每包 $b (a > b)$ 元的价格购进同样的茶叶 $25$ 包，如果以每包 $\frac{1}{3} (2 a + b)$ 元的价格全部卖出这种茶叶，那么这家商店在这次交易中（）

A、盈利了 B、亏损了 C、不盈不亏 D、不能确定

查看试题解析
9. 观察下列一组图形中的个数，其中第1个图中共有4个点，第2个图中共有10个点，第3个图中共有19个点，……，按此规律第5个图中共有点的个数是（）

A、31 B、46 C、51 D、66

查看试题解析
10. 幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方一一九宫格．将9个数填入幻方的空格中，要求每一横行、每一竖列以及两条对角线上的3个数之和相等，例如图1就是一个幻方．图2是一个未完成的幻方，则 $A - B$ 的值为（）

A、 $- 5$ B、 $- 6$ C、10 D、12

查看试题解析

二、填空题（每小题3分，共18分）下列各题不需要写出解答过程，请将结果直接填写在答题卡指定的位置．

11. ﹣2的倒数是．

查看试题解析
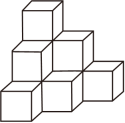
12. 已知 $| m - 1 | + {(n + 2)}^{2} = 0$ ，则 $m + n$ 的值是．

查看试题解析
13. 如图是用棱长是 $a c m$ 的小正方体组成的几何体，把这个几何体放在桌子上，并把暴露的面涂上颜色，那么涂颜色面的面积之和是 $c m^{2}$ ．

查看试题解析
14. 已知 $a$ ， $b$ 互为相反数 $(a \neq 0)$ ， $c$ ， $d$ 互为倒数， $m$ 的绝对值为 $2$ ，则代数式 $m^{2} - \frac{b}{a} + \frac{2 a + 2 b}{2023} - c d$ 的值为．

查看试题解析
15. 下列说法：
①若 $x^{2} = 1$ ，则 $x = \pm 1$ ；
②单项式 $- 2^{2} a b^{2}$ 和多项式 $x^{3} + x^{2}$ 都是五次整式；
③若 $a + b + c > 0$ ， $a b c < 0$ ，则 $\frac{| a |}{| a |} - \frac{b}{| b |} + \frac{| c |}{c} - \frac{| a b c |}{a b c}$ 的结果有两个；
④若 $2 (a x^{2} - x + 2) - (4 x^{2} + 5 x + a)$ 的运算结果中不含 $x^{2}$ 项，则常数项为 $2$ ．其中一定正确的结论是(只填序号)．

查看试题解析
16. 当 $x = 1$ 时，代数式 $p x^{2} + q x + 1$ 的值为 $20$ ，则当 $x = - 2$ 时，代数式 $- p x^{2} + 2 q x - 1$ 的值为．

查看试题解析

三、解答题（共8小题，共72分）下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形．

17. 计算：

(1)、 $- 20 + (+ 3) - (- 5) - 7$ ；

(2)、 $[{(- 1)}^{3} - 2] \times (- 5) + 4 \div (- \frac{2}{3})$ ．

查看试题解析
18. 化简：

(1)、 $- 5 a + 0.3 a + (- 2.7 a)$ ；

(2)、 $(2 a - 1) - 4 (3 - 8 a)$ ．

查看试题解析
19. 先化简，再求值： $a - 2 (a - \frac{1}{3} b^{2}) + \frac{1}{3} (b^{2} - 3)$ ，其中 $a = - 2 ， b = \frac{1}{2}$ ．

查看试题解析
20. 如图，是一所住宅的建筑平面图（图中长度单位：m）．

(1)、求这所住宅的建筑面积（用含x式子表示）；

(2)、若某市今年10月的房价均价约为15000元 $m^{2}$ ，求当图中的 $x = 6$ ， $y = 4$ 时，住户买此房产的总房价为多少万元？

查看试题解析
21. 有理数a ， b ， c在数轴上的位置如图所示．

(1)、请在数轴上表示 $- a ， - b ， - c$ ，并将a ， b ， c ， $- a ， - b ， - c$ 用“ $<$ ”连接起来；

(2)、化简： $| a | - | a - b | + | 2 c - a | - 2 | b - c |$ ．

查看试题解析
22. 最近几年时间，全球的新能源汽车发展迅猛，尤其对于我国来说，新能源汽车产销量都大幅增加．小明家新换了一辆新能源纯电动汽车，他连续 $7$ 天记录了每天行驶的路程（如表）．以 $50 k m$ 为标准，多于 $50 k m$ 的记为“ $+$ ”，不足 $50 k m$ 的记为“ $-$ ”，刚好 $50 k m$ 的记为“ $0$ ”．

第一天
第二天
第三天
第四天
第五天
第六天
第七天
路程（km）
$- 9$
$- 15$
$- 14$
0
+25
+31
+32

(1)、这 $7$ 天里路程最多的一天比最少的一天多走 $k m$ ；

(2)、请求出小明家的新能源汽车这七天一共行驶了多少千米？

(3)、已知汽油车每行驶 $100 k m$ 需用汽油 $6.5$ 升，汽油价 $8.4$ 元 $/$ 升，而新能源汽车每行驶 $100 k m$ 耗电量为 $35$ 度，每度电为 $0.56$ 元，请估计小明家换成新能源汽车后这 $7$ 天的行驶费用比原来节省多少钱？

查看试题解析
23. 观察下列三行数，回答下面的问题：

(1)、请直接写出每一行的第6个数分别是，，；

(2)、取每行数的第m个数，从上到下分别记为a ， b ， c ，则 $a + b - 4 c$ 的值为；

(3)、若用如图的“L”形框圈住4个数，其中最大数与最小数的差为2050，求这四个数中的最小数．

查看试题解析
24. 如图1，点A ， B ， C是数轴上从左到右排列的三个点，分别对应的数为 $- 2$ ， b ， 8．某同学将刻度尺如图2放置，使刻度尺上的数字0对齐数轴上的点A ，发现点B对齐刻度 $1.2 c m$ ，点C对齐刻度 $6.0 c m$ ．我们把数轴上点A到点C的距离表示为 $A C$ ，同理，A到点B的距离表示为 $A B$ ．

(1)、在图1的数轴上， $A C =$ 个长度单位；在图2中刻度尺上， $A C =$ $c m$ ；数轴上的1个长度单位对应刻度尺上的 $c m$ ；刻度尺上的 $1 c m$ 对应数轴上的个长度单位；

(2)、在数轴上点B所对应的数为b ，若点Q是数轴上一点，且满足 $C Q = 2 A B$ ，请通过计算，求b的值及点Q所表示的数；

(3)、点 $M$ ， $N$ 分别从 $B$ ， $C$ 出发，同时向右匀速运动，点 $M$ 的运动速度为5个单位长度 $/$ 秒，点 $N$ 的速度为3个单位长度 $/$ 秒，设运动的时间为 $t$ 秒 $(t > 0)$ ．在 $M$ ， $N$ 运动过程中，若 $A M - k \cdot M N$ 的值不会随 $t$ 的变化而改变，请直接写出符合条件的 $k$ 的值．

查看试题解析

	第一天	第二天	第三天	第四天	第五天	第六天	第七天
路程（km）	$- 9$	$- 15$	$- 14$	0	+25	+31	+32