湖北省咸宁市、黄冈市联考2023-2024学年九年级上学期数学期中试卷
试卷更新日期:2023-12-16 类型:期中考试
一、精心选一选(本大题共8小题,每小题3分,满分24分,在每小题给出的四个选项中只有一个符合题意,请在答题卷上将正确答案的代号涂黑)
-
1. 下列四个图片表述的是宪法赋予我们的基本权利,其图标为中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程配方后可变形为( )A、 B、 C、 D、3. 已知抛物线经过平移后得到抛物线 , 若抛物线上任意一点M坐标是 , 则其对应点坐标一定是( )A、 B、 C、 D、4. 在平面直角坐标系中的位置如图, , , , 把绕点O逆时针旋转,使点A落在y轴正半轴上,则旋转后点B的对应点的坐标为( )
2. 一元二次方程配方后可变形为( )A、 B、 C、 D、3. 已知抛物线经过平移后得到抛物线 , 若抛物线上任意一点M坐标是 , 则其对应点坐标一定是( )A、 B、 C、 D、4. 在平面直角坐标系中的位置如图, , , , 把绕点O逆时针旋转,使点A落在y轴正半轴上,则旋转后点B的对应点的坐标为( ) A、 B、 C、 D、5. 如图,已知抛物线 的对称轴是 ,直线 轴,且交抛物线于点 ,下列结论错误的是( )
A、 B、 C、 D、5. 如图,已知抛物线 的对称轴是 ,直线 轴,且交抛物线于点 ,下列结论错误的是( )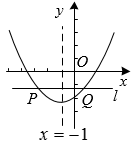 A、 B、若实数 ,则 C、 D、当 时,
A、 B、若实数 ,则 C、 D、当 时,二、细心填一填(本大题共8小题,满分24分。请把答案填在答题卷相应题号的横线上)
-
6. 方程的一次项系数是 .7. 设 , 是方程的两根,则 .8. 如图,菱形ABCD的对角线交于原点O , 点B的坐标为 , 点D的坐标为 , 则 .
 9. 二次函数中的x和y满足下表:则m的值为 .
9. 二次函数中的x和y满足下表:则m的值为 .x
……
0
1
2
3
……
y
……
0
m
0
……
10. 《代数学》中记载,形如的方程,求正数解的几何方法是:如图1,先构造一个面积为的正方形,再以正方形的边长为一边向外构造四个面积为2x的矩形,得到大正方形的面积为: , 依图1可列方程为: , 解得正数解 . 构造出如图2所示的图形,已知阴影部分的面积为50,则正数 . 11. 如图,矩形纸片ABCD , , , 将纸片ABCD折叠,使C与A重合,则折痕EF的长度为 .
11. 如图,矩形纸片ABCD , , , 将纸片ABCD折叠,使C与A重合,则折痕EF的长度为 . 12. 如图,在平面直角坐标中,对抛物线x在x轴上方的部分进行循环反复的轴对称或中心对称变换,若点A是该抛物线的顶点,则经过第2023次变换后所得的A点的坐标是 .
12. 如图,在平面直角坐标中,对抛物线x在x轴上方的部分进行循环反复的轴对称或中心对称变换,若点A是该抛物线的顶点,则经过第2023次变换后所得的A点的坐标是 .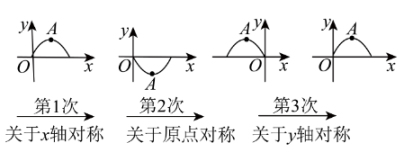 13. 如图1,E是正方形ABCD的边BC上一点(不与点B , C重合),连接AE , 以AE为边向右作正方形AEFG , 连接CF . 已知的面积(S)与BE的长(x)之间的函数关系如图2所示,若该抛物线顶点P的纵坐标为8,则正方形ABCD的边长为 .
13. 如图1,E是正方形ABCD的边BC上一点(不与点B , C重合),连接AE , 以AE为边向右作正方形AEFG , 连接CF . 已知的面积(S)与BE的长(x)之间的函数关系如图2所示,若该抛物线顶点P的纵坐标为8,则正方形ABCD的边长为 .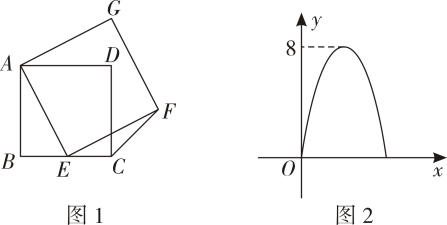
三、专心解一解(本大题共8小题,满分72分。请认真读题,冷静思考,解答题应写出必要的文字说明、证明过程或演算步骤,请把解题过程写在答题卷相应题号的位置)
-
14. 如图,在中, , , AD是的平分线,E为AD上一点,以BE为一边,且在BE下方作等边 , 连接CF .
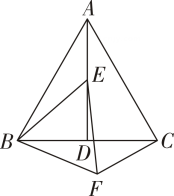 (1)、求证,;(2)、求的度数.15. 交通工程学理论用流量、速度、密度三个概念描述车流的基本特征,其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆平均速度,密度k(辆/千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段速度v(千米/小时)与密度k(辆/千米)之间关系如图所示:
(1)、求证,;(2)、求的度数.15. 交通工程学理论用流量、速度、密度三个概念描述车流的基本特征,其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆平均速度,密度k(辆/千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段速度v(千米/小时)与密度k(辆/千米)之间关系如图所示: (1)、直接写出该路段速度v(千米/小时)与密度k(辆千米)之间的函数解析式;(2)、已知q , v , k满足 . 当该路段的车辆密度k(辆)/千米)为多少时,流量达到最大?最大流量是多少?(3)、当时,该路段是较佳流量.直接写出车流密度k在什么范围时,该路段是较佳流量.16. 数学活动课上,同学们以“等腰三角形的旋转”为主题,开展如下探究活动:
(1)、直接写出该路段速度v(千米/小时)与密度k(辆千米)之间的函数解析式;(2)、已知q , v , k满足 . 当该路段的车辆密度k(辆)/千米)为多少时,流量达到最大?最大流量是多少?(3)、当时,该路段是较佳流量.直接写出车流密度k在什么范围时,该路段是较佳流量.16. 数学活动课上,同学们以“等腰三角形的旋转”为主题,开展如下探究活动: (1)、【操作探究】如图1,为等边三角形,将绕点A旋转 , 得到 , 连接BE , F是BE的中点,则;连接AF , 则AF与DE的数量关系是 .(2)、【迁移探究】如图2,将(1)中的绕点A逆时针旋转 , 得到 , 其他条件不变,求出此时的度数及AF与DE的数量关系.(3)、【拓展应用】如图3,在中, , , 将绕点A旋转,得到 , 连接BE , F是BE的中点,连接AF . 在旋转过程中,当时,线段AF的长为: .17. 如图,在平面直角坐标系中,抛物线经过、两点,其顶点为D , 连接AD , 点P是线段AD上一个动点(不与A、D重合).
(1)、【操作探究】如图1,为等边三角形,将绕点A旋转 , 得到 , 连接BE , F是BE的中点,则;连接AF , 则AF与DE的数量关系是 .(2)、【迁移探究】如图2,将(1)中的绕点A逆时针旋转 , 得到 , 其他条件不变,求出此时的度数及AF与DE的数量关系.(3)、【拓展应用】如图3,在中, , , 将绕点A旋转,得到 , 连接BE , F是BE的中点,连接AF . 在旋转过程中,当时,线段AF的长为: .17. 如图,在平面直角坐标系中,抛物线经过、两点,其顶点为D , 连接AD , 点P是线段AD上一个动点(不与A、D重合). (1)、求抛物线的函数解析式,并写出顶点D的坐标;(2)、如图,过点P作轴于点E , 连接AE , 求面积S的最大值;(3)、抛物线上是否存在一点Q , 使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.
(1)、求抛物线的函数解析式,并写出顶点D的坐标;(2)、如图,过点P作轴于点E , 连接AE , 求面积S的最大值;(3)、抛物线上是否存在一点Q , 使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.