湖北省孝感市孝南区2023-2024学年九年级上学期数学期中试卷
试卷更新日期:2023-12-16 类型:期中考试
一、精心选择,一锤定音!(每小题3分,共30分,每小题只有一个选项是正确的)
-
1. 下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 用配方法解一元二次方程的过程中,其中配方正确的是( )A、 B、 C、 D、3. 已知点与点关于原点对称,则的值为( )A、 B、 C、3 D、44. 将抛物线向右平移1个单位,再向下平移2个单位后得到的抛物线的解析式为( )A、 B、 C、 D、5. 秋冬季节是流感高发期,有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?设每轮传染中平均一个人传染了个人,则可列方程为( )A、 B、 C、 D、6. 已知二次函数()的图象如图,当时,下列说法正确的是( )
2. 用配方法解一元二次方程的过程中,其中配方正确的是( )A、 B、 C、 D、3. 已知点与点关于原点对称,则的值为( )A、 B、 C、3 D、44. 将抛物线向右平移1个单位,再向下平移2个单位后得到的抛物线的解析式为( )A、 B、 C、 D、5. 秋冬季节是流感高发期,有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?设每轮传染中平均一个人传染了个人,则可列方程为( )A、 B、 C、 D、6. 已知二次函数()的图象如图,当时,下列说法正确的是( ) A、有最小值、最大值0 B、有最小值、最大值6 C、有最小值0、最大值6 D、有最小值2、最大值67. 某种型号的小型无人机着陆后滑行的距离(米)关于滑行的时间(秒)的函数解析式是 , 无人机着陆后滑行( )秒才能停下来.A、8 B、16 C、32 D、648. 如图,边长为1的正方形绕点逆时针旋转45°后得到正方形 , 边与交于点 , 则四边形的周长是( )
A、有最小值、最大值0 B、有最小值、最大值6 C、有最小值0、最大值6 D、有最小值2、最大值67. 某种型号的小型无人机着陆后滑行的距离(米)关于滑行的时间(秒)的函数解析式是 , 无人机着陆后滑行( )秒才能停下来.A、8 B、16 C、32 D、648. 如图,边长为1的正方形绕点逆时针旋转45°后得到正方形 , 边与交于点 , 则四边形的周长是( )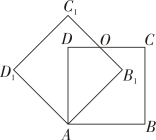 A、 B、 C、3 D、9. 如图,正方形的边长为 , 动点 , 同时从点出发,在正方形的边上,分别按 , 的方向,都以的速度运动,到达点运动终止,连接 , 设运动时间为 , 的面积为 , 则下列图象中能大致表示与的函数关系的是( )
A、 B、 C、3 D、9. 如图,正方形的边长为 , 动点 , 同时从点出发,在正方形的边上,分别按 , 的方向,都以的速度运动,到达点运动终止,连接 , 设运动时间为 , 的面积为 , 则下列图象中能大致表示与的函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、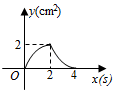 10. 二次函数(、、为常数,)中的与的部分对应值如下表:
10. 二次函数(、、为常数,)中的与的部分对应值如下表:0
3
3
3
当时,下列结论:①;②若点 , 在该抛物线上,则;③;④对于任意实数,总有 . 其中正确的结论有( )
A、3个 B、2个 C、1个 D、0个二、耐心填空,准确无误(每题3分,共计18分)
-
11. 一元二次方程化为一般形式是 .12. 抛物线的顶点坐标为 .13. 若、是方程的两实数根,则 .14. 如图,在等边中,是边上一点,连接 , 将绕点逆时针旋转60°得到 , 连接 , 若 , , 则以下四个结论中:①是等边三角形;②;③的周长是10;④ . 其中正确结论的序号为 .
 15. 若直线与二次函数的图象交于、两点,且线段 , 则 .16. 如图,是边长为2的等边三角形,点为边上的中点,以点为顶点作正方形 , 且 , 连接 , . 若将正方形绕点旋转一周,当取最小值时,的长为 .
15. 若直线与二次函数的图象交于、两点,且线段 , 则 .16. 如图,是边长为2的等边三角形,点为边上的中点,以点为顶点作正方形 , 且 , 连接 , . 若将正方形绕点旋转一周,当取最小值时,的长为 .
三、用心做一做,显显你的能力(本大题8小题,共72分)
-
17. 解方程:(1)、(2)、18. 如图,已知 , , 是直角坐标平面内三点.
 (1)、请画出关于轴对称的;(2)、请画出绕点逆时针旋转90°后的;(3)、判断以 , , 为顶点的三角形的形状为(无需说明理由).19. 如图,在中, , 将绕点A旋转一定的角度得到 , 且点E恰好落在边BC上.
(1)、请画出关于轴对称的;(2)、请画出绕点逆时针旋转90°后的;(3)、判断以 , , 为顶点的三角形的形状为(无需说明理由).19. 如图,在中, , 将绕点A旋转一定的角度得到 , 且点E恰好落在边BC上. (1)、求证:AE平分;(2)、连接BD,求证: .20. 某学校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为26米.
(1)、求证:AE平分;(2)、连接BD,求证: .20. 某学校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为26米. (1)、为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门,那么这个车棚的长和宽分别应为多少米?(2)、如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽度是多少米?21. 已知关于的方程 .(1)、求证:无论为何值,原方程都有实根;(2)、若该方程的两实根 , 为一菱形的两条对角线的长,且 , 求的值.22. 某干果店以每千克34元的价格购进一批干果,计划以每千克60元的价格销售.为尽快完成销售,决定降价促销,但售价不低于进价.经市场调查发现:这种干果的销售量(千克)与每千克降价(元)之间的函数关系如图所示.
(1)、为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门,那么这个车棚的长和宽分别应为多少米?(2)、如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽度是多少米?21. 已知关于的方程 .(1)、求证:无论为何值,原方程都有实根;(2)、若该方程的两实根 , 为一菱形的两条对角线的长,且 , 求的值.22. 某干果店以每千克34元的价格购进一批干果,计划以每千克60元的价格销售.为尽快完成销售,决定降价促销,但售价不低于进价.经市场调查发现:这种干果的销售量(千克)与每千克降价(元)之间的函数关系如图所示. (1)、求与的函数关系式,并写出自变量的取值范围;(2)、设销售总利润为(元),
(1)、求与的函数关系式,并写出自变量的取值范围;(2)、设销售总利润为(元),①求与的函数关系式;
②若 , 且最大限度让利给顾客,则这种干果应降价多少元?
(3)、若该店要求获利不低于2400元,请直接写出的取值范围.23. 是等腰直角三角形,当 , 点是射线上的任意一点(不与点重合),连接 , 如图1,将线段绕点顺时针旋转90°得线段 , 连接并延长交直线于 . (1)、猜想线段与的数量关系为 , 位置关系为;(2)、如图2,若为锐角时,其它条件不变,(1)中的结论是否成立,并说明理由;(3)、如图3,若 , , , 则的长及的面积.24. 如图1,抛物线与轴交于、两点,与轴交于 , 已知点坐标为 , 点坐标为 .
(1)、猜想线段与的数量关系为 , 位置关系为;(2)、如图2,若为锐角时,其它条件不变,(1)中的结论是否成立,并说明理由;(3)、如图3,若 , , , 则的长及的面积.24. 如图1,抛物线与轴交于、两点,与轴交于 , 已知点坐标为 , 点坐标为 . (1)、求抛物线的解析式;(2)、点为直线上方抛物线上的一点,当的面积最大时,在抛物线对称轴上找一点 , 使的和最小,求点的坐标;(3)、如图2.点为该抛物线的顶点,直线轴于点 , 在直线上是否存在点 , 使点到直线的距离等于点到点的距离?若存在,求出点的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点为直线上方抛物线上的一点,当的面积最大时,在抛物线对称轴上找一点 , 使的和最小,求点的坐标;(3)、如图2.点为该抛物线的顶点,直线轴于点 , 在直线上是否存在点 , 使点到直线的距离等于点到点的距离?若存在,求出点的坐标;若不存在,请说明理由.