湖北省武汉市新洲区阳逻街2023-2024学年九年级上学期数学期中试卷

试卷更新日期：2023-12-16 类型：期中考试

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）

1. 下列方程一定是一元二次方程的是（）

A、 $x^{2} + \frac{1}{x} + 5 = 0$ B、 $x^{2} + 3 x + y = 0$ C、 $x^{2} + x - 1 = 0$ D、 $a x^{2} + b x + c = 0$

查看试题解析
2. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 把方程 $x^{2} + 2 x = 3$ 化为 $(x + m)^{2} = n$ 的形式，则 $m$ ， $n$ 的值分別是（）

A、 $m = 1$ ， $n = 2$ B、 $m = 1$ ， $n = 3$ C、 $m = 1$ ， $n = 4$ D、 $m = - 1$ ， $n = 3$

查看试题解析
4. 将抛物线 $y = x^{2}$ 向右平移2个单位，再向上平移3个单位，则所得抛物线的解析式为（）

A、 $y = (x + 2)^{2} + 3$ B、 $y = (x - 2)^{2} + 3$ C、 $y = (x + 2)^{2} - 3$ D、 $y = (x - 2)^{2} - 3$

查看试题解析
5. 关于二次函数 $y = x^{2} + 2 x - 8$ ，下列说法正确的是（）

A、图象的对称轴在 $y$ 轴的右侧 B、图象与 $y$ 轴的交点坐标为 $(0 ， 8)$ C、当 $x > - 1$ 时， $y$ 随 $x$ 的增大而减小 D、 $y$ 的最小值为-9

查看试题解析
6. 如图，A ， B ， C ， D四个点均在⊙O上， $∠ A O D = 70 °$ ，且 $A O ∥ D C$ ，则 $∠ B$ 的度数为（）

A、40° B、45° C、50° D、55°

查看试题解析
7. 某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干、小分支的总数是73，则每个支干长出（）个小分支.

A、9 B、8 C、7 D、6

查看试题解析
8. 设拋物线 $y = a x^{2} - 2 a x - 3 a$ 上有 $A (- 2 ， y_{1})$ ， $B (\sqrt{2} ， y_{2})$ ， $C (3 ， y_{3})$ 三点，若抛物线与 $y$ 轴的交点在负半轴上，则 $y_{1}$ ， $y_{2}$ 和 $y_{3}$ 的大小关系为（）

A、 $y_{2} < y_{3} < y_{1}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{1} < y_{2} < y_{3}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
9. 如图， $⊙ O$ 的平径为 $\sqrt{5}$ ， $A B$ 与 $C D$ 为 $⊙ O$ 的两条平行弦.若 $∠ C D E = 45 °$ ， $A D = 2$ ，则弦 $B E$ 的长为（）

A、 $\frac{5}{4} \sqrt{10}$ B、 $\frac{5}{2} \sqrt{2}$ C、 $3 \sqrt{2}$ D、 $\frac{3}{2} \sqrt{5}$

查看试题解析
10. 已知二次函数 $y = x^{2} - 2023 x + 2$ 的图象上有两点 $A (a ， 1)$ 和 $B (b ， 1)$ ，则 $a^{2} - \frac{2023}{b} + 1$ 的值等于（）

A、0 B、-2023 C、2023 D、-1

查看试题解析

二、填空题（本大题共6小题，共18分）

11. 若点 $A (a ， - 3)$ 与点 $B (2 ， b)$ 关于原点对称，则 $a^{b}$ 的值为.

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ B A C = 60 °$ ，将 $△ A B C$ 绕点 $A$ 顺时针旋转 $40 °$ 得到 $△ A D E$ ，则 $∠ D A C$ 的度数为.

查看试题解析
13. 如图， $C$ 是 $\overset{⌢}{A B}$ 的中点，弦 $A B = 24$ ， $C D ⊥ A B$ ，且 $C D = 8$ ，则 $\overset{⌢}{A B}$ 所在圆的直径为.

查看试题解析
14. 一男生推铅梂，铅球出手后运动的高度 $y$ （单位：m）与水平距离 $x$ （单位：m）之间的函数关系是 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，则该男生将铅球推出的距离为m.

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = A C = 3$ ， $∠ B A C = 90 °$ ， $D$ 为边 $A B$ 上一点，将 $C D$ 绕点 $C$ 顺时针旋转 $45 °$ 得到 $C E$ ，连接 $A E$ ，则 $A E$ 长度的最小值为.

查看试题解析
16. 抛物线 $y = a x^{2} + b x + c$ （ $a$ ， $b$ ， $c$ 为常数， $c < 0)$ 经过 $(1 ， 1)$ ， $(m ， 0)$ ， $(n ， 0)$ 三点，且 $n ≥ 3$ .
下列四个结论：① $b < 0$ ；② $\frac{4 a c - b^{2}}{4 a} > 1$ ；③当 $n = 3$ 时，若点 $(2 ， t)$ 在该抛物线上，则 $t > 1$ ；④若关于x的一元二次方程 $a x^{2} + b x + c = x$ 有两个相等的实数根，则 $0 < m ≤ \frac{1}{3}$ .
其中正确的是（填序号即可）.

查看试题解析

三、解答题（本大题共8小题，共72分）

17. 解方程： $x^{2} - x - \frac{3}{4} = 0$

查看试题解析
18. 如图，平行四边形 $A B C D$ 是⊙O的内接四边形，求证：四边形 $A B C D$ 是矩形.

查看试题解析
19. 已知关于 $x$ 的一元二次方程 $x^{2} + (2 k - 3) x + k^{2} - 1 = 0$ 的两个实数根分别为 $x_{1}$ ， $x_{2}$ .

(1)、求 $k$ 的取值范围；

(2)、若 $x_{1}$ ， $x_{2}$ 满足 $x_{1}^{2} + x_{2}^{2} = 1 + x_{1} \cdot x_{2}$ ，求实数 $k$ 的值.

查看试题解析
20. 如图，四边形 $A B C D$ 为 $⊙ O$ 的内接四边形， $A C$ 为 $⊙ O$ 的直径，且 $∠ A C D$ 与 $∠ B C D$ 互余.

(1)、求证： $\overset{⌢}{C D} = \overset{⌢}{B D}$ ；

(2)、若 $C D = 2 \sqrt{5}$ ， $B C = 4$ ，求 $A B$ 的长.

查看试题解析
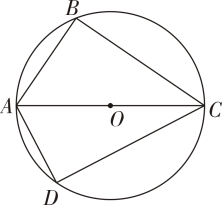21. 如图是由小正方形组成的 $7 × 5$ 网格，每个小正方形的顶点叫做格点四边形 $A B C D$ 的四个顶点都是格点，仅用无刻度的直尺在给定网格中完成画图（画图过程用虚线，画图结果用实线）.

(1)、在图1中，先在 $C D$ 上画点E ，使 $∠ A B E = 45 °$ ，再在 $A B$ 上画点F ，使 $A F = C E$ ；

(2)、在图2中，先画格点H ，使 $B H$ 平分 $∠ A B C$ （一个即可），再在 $A B$ 上画点 $G$ ，使 $A G = B C$ .

查看试题解析
22. 某网店销售一种儿童玩具，每件进价30元，规定单件销售利润不低于10元，且不高于32元.试销售期间发现，当销售单价定为40元时，每天可售出500件，销售单价每上涨1元，每天销售量减少10件，该网店决定提价销售.设销售单价为x元，每天销售量为y件.

(1)、请直接写出y与x之间的函数关系式及自变量x的取值范围；

(2)、当销售单价是多少元时，网店每天获利8360元？

(3)、网店决定每销件1件玩具，就捐赠a元（ $4 < a ≤ 8$ ）给希望工程，每天扣除捐赠后可获得最大利润为7280元，求a的值.

查看试题解析
23. 在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 120 °$ .

(1)、如图1，点 $D$ 在 $B C$ 边上，且 $∠ A D B = 2 ∠ C$ .求 $\frac{B D}{C D}$ 的值；

(2)、如图2，点 $E$ 在 $△ A B C$ 的外部，且 $2 ∠ B E C - ∠ A E B = 270 °$ .求证： $B E = \sqrt{3} A E$ ；

(3)、若 $P$ 是平面内一点，且 $∠ A P B = 90 °$ ， $∠ B P C = 150 °$ ，请直接写出 $\frac{C P}{B P}$ 的值为.

查看试题解析
24. 如图1，抛物线 $y = a x^{2} + a x - 2 a (a < 0)$ 与 $x$ 轴交于 $A$ ， $B$ 两点（点 $A$ 在点 $B$ 左边），与 $y$ 轴交于点 $C$ ，点 $P (2 ， h)$ 在抛物线上，且 $△ A B C$ 的面积为 $\frac{3}{2}$ .

(1)、求抛物线的解析式；

(2)、点D在第三象限内的抛物线上，当△ADP的面积为21时，求点D的坐标.

(3)、如图2，直线 $E F ： y = m x + n (m > 0)$ 交抛物线于 $E$ ， $F$ 两点，直线 $P F$ ， $P E$ 分别与 $y$ 轴的正、负半轴交于 $M$ ， $N$ 两点，且 $O M \cdot O N = 4$ .求证：直线 $E F$ 必过定点，并求出这个定点的坐标.

查看试题解析