2023-2024学年初中数学九年级上册 5.1 总体平均数和方差的估计同步分层训练培优卷(湘教版)

试卷更新日期：2023-12-16 类型：同步测试

进入出卷网下载

一、选择题

1. 下列说法中正确的是（）

A、一组数据2，2，3，4的中位数是2 B、一组数据的2，4，1，4，2众数是4 C、甲、乙两人进行射击测试，每人10次射击成绩的平均数均是9.1环，方差分别为：
$S_{甲}^{2} = 0.51$ ， $S_{乙}^{2} = 0.64$ ，则甲的射击成绩较稳定
D、小明的三次数学检测成绩85分，90分，97分，这三次成绩的平均数是92分

查看试题解析
2. 某公司欲招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如表：
候选人
甲
乙
丙
丁
测试成绩（百分制）
面试
$86$
$92$
$90$
$83$
笔试
$90$
$83$
$83$
$92$
如果公司认为，作为公关人员面试成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权．根据四人各自的平均成绩，公司将录取（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
3. 下图是甲、乙两名同学五次数学测试成绩的折线图.比较甲、乙两名同学的成绩，下列说法正确的是（）

A、甲同学平均分高，成绩波动较小 B、甲同学平均分高，成绩波动较大 C、乙同学平均分高，成绩波动较小 D、乙同学平均分高，成绩波动较大

查看试题解析
4. 甲、乙两个样本，计算得平均数均为10，方差 $S_{甲}^{2} = 0.102$ ， $S_{乙}^{2} = 0.06$ ，则样本的数据波动大的是（）

A、甲 B、乙 C、甲乙都一样 D、无法判断

查看试题解析
5. 学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛，各组的平时成绩的平均数（单位：分）及方差如表所示：如果要选出一个成绩较好且状态稳定的组去参赛，那么应选的组是（）

甲
乙
丙
丁
平均数
7
8
8
7
方差
1
1
1.2
1.8

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 学校招聘合唱队成员，根据实际需要，对应聘的学生进行两项素质测试，其中乐理知识成绩占 $40 %$ ，视唱练耳占 $60 %$ ，小茗乐理知识得分95，视唱练耳得分90，则小茗这次素质测试最终成绩是（　　）

A、95 B、92 C、91 D、90

查看试题解析
7. 现有12块完全相同的巧克力，每块至多被分为两小块，如果这12块巧克力可以平均分给n名同学，则n不可以为（）

A、20 B、18 C、15 D、14

查看试题解析
8. 若一组数据 $a_{1}$ ， $a_{2}$ ， $a_{3}$ 的平均数为4，方差为3，那么数据 $a_{1} + 2$ ， $a_{2} + 2$ ， $a_{3} + 2$ 的平均数和方差分别是（）

A、4， 3 B、6 $，$ 3 C、3 $，$ 4 D、6 5

查看试题解析

二、填空题

9. 已知一组数据 $x_{1}$ 、 $x_{2}$ 、 $x_{3}$ 、 $x_{4}$ 、 $x_{5}$ 的平均数是5，则另一组新数组 $x_{1} + 1$ 、 $x_{2} + 2$ 、 $x_{3} + 3$ 、 $x_{4} + 4$ 、 $x_{5} + 5$ 的平均数是．

查看试题解析
10. 甲参加某商场员工招聘，通过计算机、语言表达和商品知识三项测试，成绩分别为：85、90、92，若相应分别按 $20 % 、 30 % 、 50 %$ 的比例计算成绩，则甲的综合得分为分．

查看试题解析
11. 某餐饮外卖平台规定，点单时除点餐费用外，需另付配送费6元．某学习小组统计了一段时间内该外卖平台的部分订单中，每单的消费总额和每单不计算配送费的消费额的数据，对于两种情况得到的两组数据有如下3个判断：①众数不同；②中位数不同；③平均数相同．其中所有正确判断的序号是．

查看试题解析
12. 学校组织一分钟跳绳比赛．八（1）班准备从甲、乙两人中挑选一名成绩比较稳定的同学参赛．两人最近四次的跳绳测试的成绩（单位：个）为：甲：197，213，209，196；乙：205，203，202，205，而这两人平均成绩相同，根据信息，应该选参加比赛．

查看试题解析
13. 已知一组数据23，25，20，15，x，15，若它们的中位数是21，那么它们的平均数为。

查看试题解析

三、解答题

14. 某商场为了了解A产品的销售情况，在上个月的销售记录中，随机抽取了5天A产品的销售记录，其售价x（元/件）与对应销量 y（件）的全部数据如下表：
售价x（元/件）
80
85
90
95
100
销量y（件）
110
100
80
60
50
试求这5天中A产品平均每件的售价．

查看试题解析
15. 已知一组数据：x，10，12，6的中位数与平均数相等，求x的值。

查看试题解析

四、综合题

16. 我市某中学举办“网络安全知识答题竞赛”，初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．

	平均分 $（$ 分 $）$	中位数 $（$ 分 $）$	众数 $（$ 分 $）$	方差（ $分^{2}$ ）
初中部	$a$	$85$	$b$	$S_{初中}^{2}$
高中部	$85$	$c$	$100$	$160$

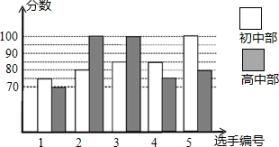(1)、根据图示计算出

a

、

b

、

c

的值；

(2)、结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？

(3)、计算初中代表队决赛成绩的方差

s_{初 中}^{2}

，并判断哪一个代表队选手成绩较为稳定．

查看试题解析

17. 为了了解甲、乙、丙三种型号的扫地机器人的扫地质量，工作人员从某月生产的甲、乙、丙三种型号扫地机器人中各随机抽取10台，在完全相同条件下试验，记录下它们的除尘指数的数据，并进行整理、描述和分析，下面给出了部分信息．
ⅰ.甲、乙两种型号扫地机器人除尘指数的折线图：

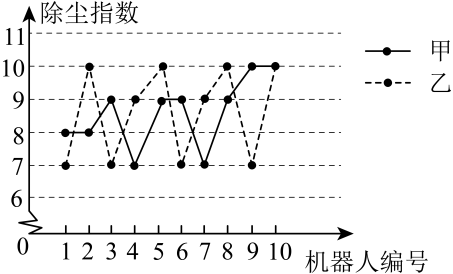
ⅱ.丙型号扫地机器人的除尘指数数据：10，10，10，9，9，8，3，9，8，10.

ⅲ．甲、乙、丙三种型号机器人除尘指数的平均数：

扫地机器人

甲

乙

丙

除尘指数平均数

8.6

8.6

m

根据以上信息，回答下列问题：

(1)、求表中m的值；

(2)、在抽取的扫地机器人中，如果除尘指数的10个数据的方差越小，则认为该型号的扫地机器人性能更稳定．据此推断：在甲、乙两种型号扫地机器人中，型扫地机器人的性能稳定（填“甲”或“乙”）；

(3)、在抽取的扫地机器人中，如果把10个除尘指数去掉一个最高值和一个最低值之后的平均值作为性能参考，平均值越高，则认为该型号扫地机器人性能表现越优秀．据此推断：在甲、乙、丙三种型号的扫地机器人中，表现最优秀的是（填“甲”、“乙”或“丙”）．

查看试题解析

候选人		甲	乙	丙	丁
测试成绩（百分制）	面试	$86$	$92$	$90$	$83$
测试成绩（百分制）	笔试	$90$	$83$	$83$	$92$

	甲	乙	丙	丁
平均数	7	8	8	7
方差	1	1	1.2	1.8

售价x（元/件）	80	85	90	95	100
销量y（件）	110	100	80	60	50

扫地机器人	甲	乙	丙
除尘指数平均数	8.6	8.6	m

2023-2024学年初中数学九年级上册 5.1 总体平均数和方差的估计 同步分层训练培优卷(湘教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 5.1 总体平均数和方差的估计同步分层训练培优卷(湘教版)