2023-2024学年初中数学九年级上册 4.4 解直角三角形的应用同步分层训练培优卷(湘教版)

试卷更新日期：2023-12-16 类型：同步测试

进入出卷网下载

一、选择题

1. 学校开放日即将来临，负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳 $A B$ 到地面，如图所示．已彩旗绳与地面形成 $25 °$ 角（即 $∠ B A C = 25 °$ ）、彩旗绳固定在地面的位置与图书馆相距32米（即 $A C = 32$ 米），则彩旗绳 $A B$ 的长度为（）

A、 $32 s i n 25 °$ 米 B、 $32 c o s 25 °$ 米 C、 $\frac{32}{s i n 25 °}$ 米 D、 $\frac{32}{c o s 25 °}$ 米

查看试题解析
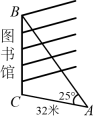2. “儿童放学归来早，忙趁东风放纸鸢”，小明周末在龙潭公园草坪上放风筝，已知风筝拉线长100米且拉线与地面夹角为 $65 °$ （如图所示，假设拉线是直的，小明身高忽略不计），则风筝离地面的高度可以表示为（）

A、 $100 s i n 65 °$ B、 $100 c o s 65 °$ C、 $100 t a n 65 °$ D、 $\frac{100}{s i n 65 °}$

查看试题解析
3. 某驱逐舰在海上执行任务后刚返回到港口A，接到上级指令，发现在其北偏东 $30 °$ 方向上有一艘可疑船只C，与此同时在港口A处北偏东 $60 °$ 方向上且距离 $10 k m$ 处有另一艘驱逐舰B也收到了相关指令，驱逐舰B恰好在可疑船只C的南偏东 $30 °$ 的方向上，则可疑船只C距离港口A的距离为（　　）

A、 $\frac{5 \sqrt{3}}{3} k m$ B、 $\frac{10 \sqrt{3}}{3} k m$ C、 $\frac{20 \sqrt{3}}{3} k m$ D、 $10 \sqrt{3} k m$

查看试题解析
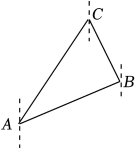4. 如图，某天下午2时，两艘船只分别从港口O点处出发，其中快船沿北偏东 $3 0^{∘}$ 方向以2海里/时的速度行驶，慢船沿北偏西 $6 0^{∘}$ 方向以1海里/时的速度行驶，当天下午4时，两艘船只分别到达A，B两点，则此时两船之间的距离等于（）

A、 $\sqrt{5}$ 海里 B、 $\sqrt{3}$ 海里 C、2 $\sqrt{3}$ 海里 D、2 $\sqrt{5}$ 海里

查看试题解析
5. 如图是某区域的平面示意图，码头A在观测站B的正东方向，码头A的北偏西60°方向上有一小岛C，小岛C在观测站B的北偏西15°方向上，码头A到小岛C的距离AC为 $(\sqrt{3} + 1)$ 海里.观测站B到AC的距离BP是（）

A、 $\sqrt{3}$ B、1 C、2 D、 $\frac{\sqrt{3} + 1}{2}$

查看试题解析
6. 如图，某商场一楼与二楼之间的电梯示意图.∠ABC=150°，BC的长是8m，则乘电梯从点B到点C上升的高度h是（）

A、 $\frac{8}{3} \sqrt{3}$ m B、 $4 \sqrt{3}$ m C、8m D、4m

查看试题解析
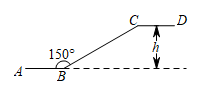7. 消防云梯如图所示，AB⊥BC于B，当C点刚好在A点的正上方时，DF的长是.（）

A、 $a c o s θ + b s i n θ$ B、 $a c o s θ + b t a n θ$ C、 $\frac{a}{c o s θ} + b s i n θ$ D、 $\frac{a}{c o s θ} + \frac{b}{s i n θ}$

查看试题解析
8. 如图， $△ A B C$ 中， $A B = A C = 10$ ， $t a n A = 3$ ， $B D ⊥ A C$ 于点 $D$ ，若点 $E$ 是线段 $B D$ 上一动点，则 $C E + \frac{\sqrt{10}}{10} B E$ 的最小值为（）

A、 $3 \sqrt{10}$ B、 $\frac{3 \sqrt{10}}{2}$ C、 $5 \sqrt{3}$ D、 $10$

查看试题解析

二、填空题

9. 综合实践课上，航模小组用航拍无人机进行测高实践．如图，无人机从地面 $C D$ 的中点A处竖直上升30米到达B处，测得博雅楼顶部E的俯角为 $45 °$ ，尚美楼顶部F的俯角为 $30 °$ ，已知博雅楼高度 $C E$ 为15米，则尚美楼高度 $D F$ 为米．（结果保留根号）

查看试题解析
10. 如图， $△ A B C$ 中， $∠ A = 60 °$ ， $A C > A B > 6$ ，点D，E分别在边 $A B$ ， $A C$ 上，且 $B D = C E = 6$ ，连接 $D E$ ，点M是 $D E$ 的中点，点N是BC的中点，线段MN的长为．

查看试题解析
11. 如图，供给船要给C岛运送物资，从海岸线AB的港口A出发向北偏东40°方向直线航行60nmile到达C岛．测得海岸线上的港口B在C岛南偏东50°方向．若A，B两港口之间的距离为65nmile，则C岛到港口B的距离是nmile．

查看试题解析
12. 如图1是一个消防云梯，其示意图如图2所示，此消防云梯由救援台AB，延展臂BC（B在C的左侧），伸展主臂CD，支撑臂EF构成.在操作过程中，救援台AB，车身GH及地面MN三者始终保持平行，

(1)、当∠EFH＝55°，BC∥EF时，∠ABC＝度；

(2)、如图3为了参与另一项高空救援工作，需要进行调整，使得延展臂BC与支撑臂EF
所在直线互相垂直，且∠EFH＝78°，此时∠ABC＝度．

查看试题解析
13. 如(图1)，某学校楼梯墙面上悬挂了四幅全等的正方形画框，画框下边缘与 $B$ 水平地面平行．如(图2)，画框的左上角顶点 $B$ ， $E$ ， $F$ ， $G$ 都在直线 $A B$ 上，且 $B E = E F = F G$ ，楼梯装饰线条所在直线 $C D / / A B$ ，延长画框的边 $B H$ ， $M N$ 得到平行四边形ABCD．若直线 $P Q$ 恰好经过点 $D$ ， $A B = 275 c m$ ， $C H = 100 c m$ ， $∠ A = 60 °$ ，则正方形画框的边长为

查看试题解析

三、解答题

14. 如图1，是某校教学楼正厅一角处摆放的“教学楼平面示意图”展板，数学学习小组想要测量此展板的最高点到地面的高度．他们绘制了图2所示的展板侧面的截面图，并测得 $A B = 120 c m$ ， $B D = 80 c m$ ， $∠ A B D = 105 °$ ， $∠ B D Q = 60 °$ ，底座四边形 $E F P Q$ 为矩形， $E F = 5 c m$ ．请帮助该数学学习小组求出展板最高点A到地面 $P F$ 的距离．（结果精确到 $1 c m$ ．参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
15. 如图，某数学兴趣小组为了测量古树 $D E$ 的高度，采用了如下的方法：先从与古树底端 $D$ 在同一水平线上的点A出发，沿斜面坡度为 $i = 2 ： \sqrt{3}$ 的斜坡 $A B$ 前进 $20 \sqrt{7} m$ 到达点 $B$ ，再沿水平方向继续前进一段距离后到达点 $C$ ．在点 $C$ 处测得古树 $D E$ 的顶端 $E$ 的俯角为 $37 °$ ，底部 $D$ 的俯角为 $60 °$ ，求古树 $D E$ 的高度（参考数据： $s i n 37 ° \approx \frac{3}{5}$ ， $c o s 37 ° \approx \frac{4}{5}$ ， $t a n 37 ° \approx \frac{3}{4}$ ，计算结果用根号表示，不取近似值）．

查看试题解析

四、综合题

16. 如图，光从空气斜射入水中，入射光线 $A B$ 射到水池的水面 $B$ 点后折射光线 $B D$ 射到池底点 $D$ 处，入射角 $∠ A B M = 30 °$ ，折射角 $∠ D B N = 22 °$ ；入射光线 $A C$ 射到水池的水面 $C$ 点后折射光线 $C E$ 射到池底点 $E$ 处，入射角 $∠ A C M' = 60 °$ ，折射角 $∠ E C N' = 40.5 ° . D E / / B C$ ， $M N$ 、 $M' N'$ 为法线 $.$ 入射光线 $A B$ 、 $A C$ 和折射光线 $B D$ 、 $C E$ 及法线 $M N$ 、 $M' N'$ 都在同一平面内，点 $A$ 到直线 $B C$ 的距离为 $6$ 米．

(1)、求 $B C$ 的长； $($ 结果保留根号 $)$

(2)、如果 $D E = 8.72$ 米，求水池的深 $. ($ 参考数据： $\sqrt{2}$ 取 $1.41$ ， $\sqrt{3}$ 取 $1.73$ ， $s i n 22 °$ 取 $0.37$ ， $c o s 22 °$ 取 $0.93$ ， $t a n 22 °$ 取 $0.4$ ， $s i n 40.5 °$ 取 $0.65$ ， $c o s 40.5 °$ 取 $0.76$ ， $t a n 40.5 °$ 取 $0.85)$

查看试题解析
17. 如图，等腰 $△ A B C$ 的底边 $B C = 8$ ，高 $A D = 2$ ， M是 $A B$ 的中点，连接 $M D$ ．动点E从点B出发，以每秒1个单位的速度沿 $B C$ 向点C运动，到点C停止；另一动点F从点B出发，以相同的速度沿 $B C$ 运动，到点D停止.已知点E比点F早出发1秒，当点F出发后，以 $E F$ 为边作正方形 $E F G H$ ，使G，H和点A在 $B C$ 的同侧，设点E运动的时间为t秒．

(1)、当 $t \geq 1$ 时，用含t的代数式表示 $E F$ 的长；

(2)、设正方形 $E F G H$ 面积为 $S_{1}$ ，正方形 $E F G H$ 与 $△ A B C$ 重叠面积为 $S_{2}$ ，当 $S_{1} ： S_{2} = 2$ 时，求t的值；

(3)、在点F开始运动时，点P从点D出发，以每秒 $2 \sqrt{5}$ 个单位的速度沿折线段 $D M - M B - B M - M D$ ，到达点D停止，在点E的整个运动过程中，求点P在正方形 $E F G H$ 内（含边界）的时长．

查看试题解析

2023-2024学年初中数学九年级上册 4.4 解直角三角形的应用 同步分层训练培优卷(湘教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 4.4 解直角三角形的应用同步分层训练培优卷(湘教版)