2023-2024学年初中数学九年级上册 4.4 解直角三角形的应用 同步分层训练基础卷(湘教版)
试卷更新日期：2023-12-16 类型：同步测试
一、选择题
-
1. 淇淇一家要到革命圣地西柏坡参观．如图，西柏坡位于淇淇家南偏西的方向，则淇淇家位于西柏坡的（ ）
A、南偏西方向 B、南偏东方向 C、北偏西方向 D、北偏东方向2. 爬坡时坡角与水平面夹角为α，则每爬1m耗能 ， 若某人爬了1000m，该坡角为30°，则他耗能（ ）.（参考数据： ， ）
A、58J B、159J C、1025J D、1732J3. 松华坝水库地处昆明北郊，是昆明市的重要水源，被称为“昆明头上的一碗水”，水库周边遍布森林与湿地，呈现出一幅纯净自然的和谐生态画卷．如图，大坝某段横截面迎水坡的坡度（），若坝高 ， 则坡面的水平宽度长度约为（ ）（参考数据： ， ， ）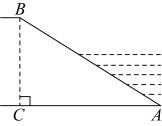
A、 B、 C、 D、4. 如果某个斜坡的坡度是 ， 那么这个斜坡的坡角为（ ）A、30° B、45° C、60° D、90°5. 如图，一航班沿北偏东方向从A地飞往C地，到达C地上空时，由于天气情况不适合着陆，准备备降B地，已知C地在B地的北偏西方向，则其改变航向时的度数为（ ）
A、 B、 C、 D、6. 如图，小兵同学从处出发向正东方向走米到达处，再向正北方向走到处，已知 ， 则 ， 两处相距（ ）
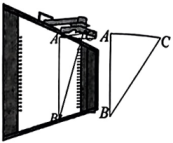
A、米 B、米 C、米 D、米7. 如图，在平面直角坐标系中， ， ， 点C在x轴正半轴上，点D在y轴正半轴上，且 ， 以为直径的第一象限作半圆，交线段于点E、F ， 则线段的最大值为（ ）
A、 B、 C、 D、8. 如图，一辆自行车竖直摆放在水平地面上，右边是它的部分示意图，现测得∠A＝88°，∠C＝42°，AB＝60，则点A到BC的距离为（ ）
A、60sin50° B、 C、60cos50° D、60tan50°二、填空题
-
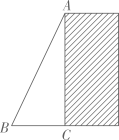
9. 如图，大坝横截面迎水坡AB的坡比为2：1，若坝高AC为12（m），则迎水坡AB的长为 （m）．
10. 某数学活动小组要测量一建筑物的高度，如图，他们在建筑物前的平地上选择一点 ， 在点和建筑物之间选择一点 ， 测得 ． 用高的测角仪在处测得建筑物顶部的仰角为 ， 在处测得仰角为 ， 则该建筑物的高是 ．
11. 如图，一航班沿北偏东方向从地飞往地，到达地上空时，由于天气情况不适合着陆，准备备降地，已知地在地的北偏西方向，则其改变航向时的度数为 ．
12. 某校九年级的一位同学，想利用刚刚学过的三角函数知识测量新教学楼的高度，如图，她在A处测得新教学楼房顶B点的仰角为45°，走6米到C处再测得B点的仰角为55°，已知O、A、C在同一条直线上，则新教学楼的高度OB是米.（结果根据“四舍五入”法保留小数点后两位）（参考数据：sin55°≈0.82，cos55°≈0.57，tan55°≈1.43）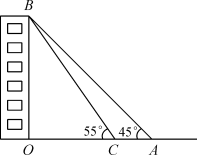
13. 在一次综合实践活动中，某学校数学兴趣小组对一电视发射塔的高度进行了测量．如图，在塔前C处，测得该塔顶端B的仰角为 ， 后退（）到D处有一平台，在高（）的平台上的E处，测得B的仰角为 ． 则该电视发射塔的高度为 ． （精确到 ． 参考数据：）
三、解答题
-
14. 教室里的投影仪投影时，可以把投影光线CA，CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC， ． 黑板上投影图像的高度 ， CB与AB的夹角 ， 求AC的长．（结果精确到1cm．参考数据： ， ， ）
15. 某次军事演习中，一艘船以千米每小时的速度向正东航行，在出发地测得小岛在它的北偏东方向，小时后到达处测得小岛在它的北偏西方向，求该船在航行到B处时与小岛C的距离．（结果保留根号）
四、综合题
-
16. 如图，在中， ， ， ， 动点从点出发，沿线段的方向以每秒1单位长度的速度向终点A运动，以点P为旋转中心，将线段顺时针旋转90°，得到线段 ， 连接 ， 设与重合部分的面积为 ， 点P运动时间为秒（）．
(1)、；(2)、当点落在上时，求的值；(3)、点运动过程中，求与的关系式；(4)、当点与的一个顶点的连线所在直线平分面积时，直接写出此时的值．17. 小亮利用所学的知识对大厦的高度进行测量，他在自家楼顶B处测得大厦底部的俯角是 ， 测得大厦顶部的仰角是 ， 已知他家楼顶B处距地面的高度为40米（图中点A ， B ， C ， D均在同一平面内）．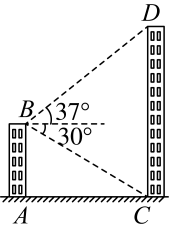
(1)、求两楼之间的距离（结果保留根号）；(2)、求大厦的高度（结果取整数）．（参考数据： ， ， ， ）