2023-2024学年初中数学九年级上册 4.3 解直角三角形 同步分层训练培优卷(湘教版)
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为( )
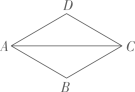 A、 B、1 C、 D、2. 如图,在中, , 设所对的边边长分别为a,b,c,则下列等式正确的是( )
A、 B、1 C、 D、2. 如图,在中, , 设所对的边边长分别为a,b,c,则下列等式正确的是( )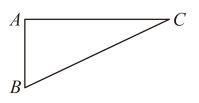 A、 B、 C、 D、3. 一沙滩球网支架示意图如图所示,AB=AC=a米,∠ABC=a,则最高点A离地面BC的高度为( )
A、 B、 C、 D、3. 一沙滩球网支架示意图如图所示,AB=AC=a米,∠ABC=a,则最高点A离地面BC的高度为( ) A、米 B、米 C、米 D、米4. 如图,在正方形ABCD中,点E在边BC上(不与点B,C重合),点F在边AB上,且AF=BE,连接AE,DF,对角线AC与DF交于点G,连接BG,交AE于点H.若DF=4GH,则= ( )
A、米 B、米 C、米 D、米4. 如图,在正方形ABCD中,点E在边BC上(不与点B,C重合),点F在边AB上,且AF=BE,连接AE,DF,对角线AC与DF交于点G,连接BG,交AE于点H.若DF=4GH,则= ( ) A、 B、 C、 D、5. 如图,中, , , , 平分交于点D,分别过点D作于E,于F,则四边形的面积为( )
A、 B、 C、 D、5. 如图,中, , , , 平分交于点D,分别过点D作于E,于F,则四边形的面积为( ) A、12 B、16 C、 D、6. 如图所示,菱形 的周长为 , , 垂足为E, , 则下列结论正确的个数有( )
A、12 B、16 C、 D、6. 如图所示,菱形 的周长为 , , 垂足为E, , 则下列结论正确的个数有( )
① , ② , ③菱形的面积为 , ④.
A、1个 B、2个 C、3个 D、4个7. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( ) A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤8. 在平面直角坐标系中,点A在直线l上,以A为圆心,为半径的圆与y轴的另一个交点为E,给出如下定义:若线段 , 和直线l上分别存在点B,点C和点D,使得四边形是矩形(点顺时针排列),则称矩形为直线l的“理想矩形”.例如,右图中的矩形为直线l的“理想矩形”.若点 , 则直线的“理想矩形”的面积为( )
A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤8. 在平面直角坐标系中,点A在直线l上,以A为圆心,为半径的圆与y轴的另一个交点为E,给出如下定义:若线段 , 和直线l上分别存在点B,点C和点D,使得四边形是矩形(点顺时针排列),则称矩形为直线l的“理想矩形”.例如,右图中的矩形为直线l的“理想矩形”.若点 , 则直线的“理想矩形”的面积为( )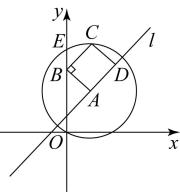 A、12 B、 C、 D、
A、12 B、 C、 D、二、填空题
-
9. 如图,与位于平面直角坐标系中, , , , 若 , 反比例函数恰好经过点C,则 .
 10. 如图,将的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为cm
10. 如图,将的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为cm(结果精确到0.1cm,参考数据: , , )
 11. 如图.四边形中, , , , 交于点 , , , 则AB的长为 .
11. 如图.四边形中, , , , 交于点 , , , 则AB的长为 .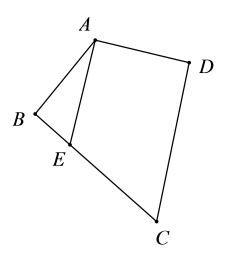 12. 一副直角三角板如图放置,点在的延长线上, , 则°.
12. 一副直角三角板如图放置,点在的延长线上, , 则°.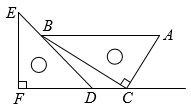 13. 如图,在等边中,过点C作射线 , 点M,N分别在边 , 上,将沿折叠,使点B落在射线上的点处,连接 , 已知 . 给出下列四个结论:①为定值;②当时,四边形为菱形;③当点N与C重合时,;④当最短时, . 其中正确的结论是(填写序号)
13. 如图,在等边中,过点C作射线 , 点M,N分别在边 , 上,将沿折叠,使点B落在射线上的点处,连接 , 已知 . 给出下列四个结论:①为定值;②当时,四边形为菱形;③当点N与C重合时,;④当最短时, . 其中正确的结论是(填写序号)
三、解答题
-
14. 如图,在中,已知 . 点为边上一点, , 求的长.
 15. 根据以下素材,探索完成任务.
15. 根据以下素材,探索完成任务.探究遮阳伞下的影子长度
素材1
图1是某款自动旋转遮阳伞,伞面完全张开时张角呈 , 图2是其侧面示意图.已知支架AB长为2.5米,且垂直于地面BC,悬托架米,点E固定在伞面上,且伞面直径DF是DE的4倍.当伞面完全张开时,点D,E,F始终共线.为实现遮阳效果最佳,伞面装有接收器可以根据太阳光线的角度变化,自动调整手柄D沿着AB移动,以保证太阳光线与DF始终垂直.

素材2
时刻
12点
13点
14点
15点
16点
17点
太阳高度(度)
90
75
60
45
30
15
参考数据: , .
某地区某天下午不同时间的太阳高度角(太阳光线与地面的夹角)参照表:
素材3
小明坐在露营椅上的高度(头顶到地面的距离)约为1米.如图2,小明坐的位置记为点Q.
问题解决
任务1
确定影子长度
某一时刻测得米,请求出此时影子的长度.
任务2
判断是否照射到
这天14点,小明坐在离支架3米处的Q点,请判断此时小明是否会被太阳光照射到?
任务3
探究合理范围
小明打算在这天14:00-15:00露营休息,为保证小明全程不被太阳光照射到,请计算的取值范围.
四、综合题
-
16. 是等边三角形,点是射线上的一点(不与点 , 重合),连接 , 在的左侧作等边三角形 , 将线段绕点逆时针旋转 , 得到线段 , 连接 . 交于点 .
 (1)、如图1,当点为中点时,请直接写出线段与的数量关系;(2)、如图2.当点在线段的延长线上时,请判断()中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、当 , 时,请直接写出的长.17. 如图1,在菱形中, . 等腰的两个顶点分别在上,且 , 点在的异侧.
(1)、如图1,当点为中点时,请直接写出线段与的数量关系;(2)、如图2.当点在线段的延长线上时,请判断()中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、当 , 时,请直接写出的长.17. 如图1,在菱形中, . 等腰的两个顶点分别在上,且 , 点在的异侧.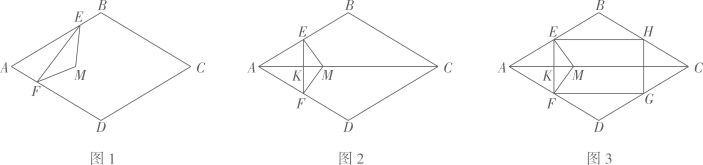 (1)、如图2,当于点时,
(1)、如图2,当于点时,①求证: , 且点在菱形的对角线上.
②如图3,若交于点交于点 , 连结 . 当 时,四边形为正方形.
(2)、如图1,①判断:点 ▲ 菱形的对角线上.(填“在”或“不在”)
②若 , 请求出的取值范围.