2023-2024学年初中数学九年级上册 4.2 正切 同步分层训练培优卷(湘教版)
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 如图,在中, , , 是腰上的高,则的长( )
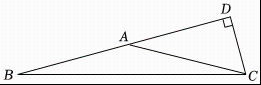 A、 B、 C、 D、2. 下图源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为 , 则的值为( )
A、 B、 C、 D、2. 下图源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为 , 则的值为( ) A、 B、 C、 D、3. 如图,在离铁塔100米的A处,用测倾仪测得塔顶的仰角为 , 测倾仪高为1.4米,则铁塔的高为( )
A、 B、 C、 D、3. 如图,在离铁塔100米的A处,用测倾仪测得塔顶的仰角为 , 测倾仪高为1.4米,则铁塔的高为( ) A、米 B、米 C、米 D、米4. 已知,如图,点A是直线上一点,过点A作x轴平行线,与反比例函数交于点B , 以为边向下作 , 点C恰好在轴上,且 , , 若的面积为 , 则的值为( )
A、米 B、米 C、米 D、米4. 已知,如图,点A是直线上一点,过点A作x轴平行线,与反比例函数交于点B , 以为边向下作 , 点C恰好在轴上,且 , , 若的面积为 , 则的值为( )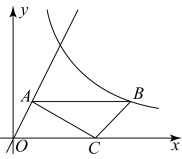 A、 B、2 C、 D、5. 如图,已知矩形纸片ABCD,其中 , 现将纸片进行如下操作:
A、 B、2 C、 D、5. 如图,已知矩形纸片ABCD,其中 , 现将纸片进行如下操作:第一步,如图①将纸片对折,使AB与DC重合,折痕为EF,展开后如图②;
第二步,再将图②中的纸片沿对角线BD折叠,展开后如图③;
第三步,将图③中的纸片沿过点E的直线折叠,使点C落在对角线BD上的点H处,如图④.
则DH的长为( ) A、 B、 C、 D、6. 如图,由边长为1的小正方形组成的网格中,的三个顶点A,B,C都在网格的格点上,则下列结论错误的是( )
A、 B、 C、 D、6. 如图,由边长为1的小正方形组成的网格中,的三个顶点A,B,C都在网格的格点上,则下列结论错误的是( )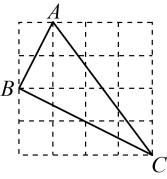 A、 B、 C、 D、7. 如图,在矩形ABCD中,.把AD沿AE折叠,使点恰好落在AB边上的处,再将绕点顺时针旋转 , 得到 , 使得恰好经过的中点.设交AB于点 , 连接.有如下结论:①;②的长度是;③;④.上述结论中,正确的个数有( )
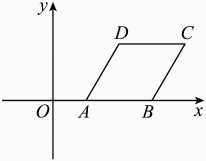
A、 B、 C、 D、7. 如图,在矩形ABCD中,.把AD沿AE折叠,使点恰好落在AB边上的处,再将绕点顺时针旋转 , 得到 , 使得恰好经过的中点.设交AB于点 , 连接.有如下结论:①;②的长度是;③;④.上述结论中,正确的个数有( ) A、1个 B、2个 C、3个 D、4个8. 如图,矩形中, , 以点B为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线 , 过点C作的垂线分别交于点M,N,则的长为( )
A、1个 B、2个 C、3个 D、4个8. 如图,矩形中, , 以点B为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线 , 过点C作的垂线分别交于点M,N,则的长为( )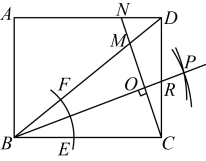 A、 B、 C、 D、4
A、 B、 C、 D、4二、填空题
-
9. 如图,在平面直角坐标系中,菱形的顶点A,B在x轴上, , , , 将菱形绕点A旋转后,得到菱形 , 则点的坐标是 .
 10. 计算: .11. 如图,在中, . 以点为圆心,以的长为半径作弧交边于点 , 连接 . 分别以点为圆心,以大于的长为半径作弧,两弧交于点 , 作射线交于点 , 交边于点 , 则的值为 .
10. 计算: .11. 如图,在中, . 以点为圆心,以的长为半径作弧交边于点 , 连接 . 分别以点为圆心,以大于的长为半径作弧,两弧交于点 , 作射线交于点 , 交边于点 , 则的值为 .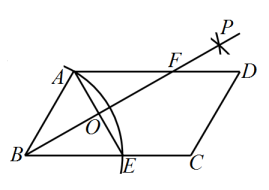 12. 如图,在中,斜边 , , 的垂直平分线分别交、于点E、点D , 连接 , 点M , N分别是和上的动点,则的最小值是 .
12. 如图,在中,斜边 , , 的垂直平分线分别交、于点E、点D , 连接 , 点M , N分别是和上的动点,则的最小值是 . 13. 如图,在中, , 点D为边的中点,点E在边上, , 将沿BE折叠至 , 当时,则 .
13. 如图,在中, , 点D为边的中点,点E在边上, , 将沿BE折叠至 , 当时,则 .
三、解答题
-
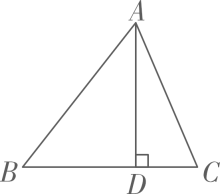
14. 如图,在△ABC中,AD⊥BC ,垂足是点D,若BC=14,AD=12,tan∠BAD= , 求sinC的值.
 15. 先化简,再求代数式的值,其中 .
15. 先化简,再求代数式的值,其中 .四、综合题
-
16. 已知菱形ABCD和等边△CEF,∠ABC=60°,
 (1)、当E,F分别在CA,CB的延长线上时(如图1),连结AF,DE.
(1)、当E,F分别在CA,CB的延长线上时(如图1),连结AF,DE.①求证:AF=DE:
②连结DF,交AB于点N(如图2),取AE的中点M,连结MN.若AE=AC=3,求MN的长:
(2)、当点F在DA的延长线上时(如图3),连结AE,DE,分别取AE,DF的中点M,N,连结MN.若AC=2,CE= , 求MN的长,17. 数学活动课上,老师组织数学小组的同学进行以“三角形卡片拼接与变换”为主题的数学学习活动.他们准备若干个 , 的特殊直角三角形卡片,其中在三角形卡片中, , , . (1)、如图1,将一个与全等的沿较长的直角边重合,拼成一个四边形 .
(1)、如图1,将一个与全等的沿较长的直角边重合,拼成一个四边形 .①求证:四边形是平行四边形;
②连接交于点 , 求的面积;
(2)、在(1)的条件下,将一条直角边与重合的等腰直角三角形卡片与四边形拼成如图2所示的平面图形,请求出点到的距离;(3)、一个斜边长度与相等的三角板( , )如图3摆放,将绕点A顺时针旋转,旋转角为 , 旋转后的三角形记为 . 在旋转过程中,直线所在的直线与直线 , 交于 , 两点,当为等腰三角形时,请直接写出的长.