2023-2024学年初中数学九年级上册 4.2 正切 同步分层训练基础卷(湘教版)
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 的值等于( )A、1 B、 C、 D、22. 如图,某段河流的两岸互相平行,为测量此段的河宽(与河岸垂直),测得两点的距离为米, , 则河宽的长为( )
 A、 B、 C、 D、3. 如图,某飞机于空中A处探测到正下方的地面目标C , 此时飞机高度为1400米,从飞机上看地面控制点B的俯角为 , 则B、C之间的距离为( )
A、 B、 C、 D、3. 如图,某飞机于空中A处探测到正下方的地面目标C , 此时飞机高度为1400米,从飞机上看地面控制点B的俯角为 , 则B、C之间的距离为( )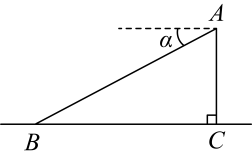 A、米 B、米 C、米 D、米4. 已知是锐角, , 则的值为( )A、30° B、60° C、45° D、无法确定5. 如图,某商场有一自动扶梯,其倾斜角为 , 高为7米.用计算器求的长,下列按键顺序正确的是( )
A、米 B、米 C、米 D、米4. 已知是锐角, , 则的值为( )A、30° B、60° C、45° D、无法确定5. 如图,某商场有一自动扶梯,其倾斜角为 , 高为7米.用计算器求的长,下列按键顺序正确的是( )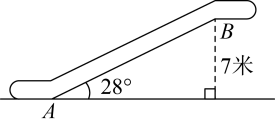 A、
A、 B、
B、 C、
C、 D、
D、 6. 延时课上,王林用四根长度都为的木条制作了图1所示正方形,而后将正方形的边固定,平推成图2的图形,并测得 , 在此变化过程中结论错误的是( )
6. 延时课上,王林用四根长度都为的木条制作了图1所示正方形,而后将正方形的边固定,平推成图2的图形,并测得 , 在此变化过程中结论错误的是( )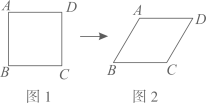 A、长度不变,为 B、长度变小,减少 C、面积变小,减少 D、长度变大,增大7. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形()和中间一个小正方形拼成的大正方形中, , 连接 . 设 , 若正方形与正方形的面积之比为 , 则( )
A、长度不变,为 B、长度变小,减少 C、面积变小,减少 D、长度变大,增大7. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形()和中间一个小正方形拼成的大正方形中, , 连接 . 设 , 若正方形与正方形的面积之比为 , 则( ) A、5 B、4 C、3 D、28. 如图,在平面直角坐标系中,四边形OABC的顶点在原点上,OA边在轴的正半轴上,轴, , 将四边形OABC绕点送时针旋转,每次旋转 , 则第2023次旋转结束时,点的坐标为( )
A、5 B、4 C、3 D、28. 如图,在平面直角坐标系中,四边形OABC的顶点在原点上,OA边在轴的正半轴上,轴, , 将四边形OABC绕点送时针旋转,每次旋转 , 则第2023次旋转结束时,点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
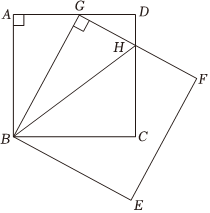
9. 如图,已知正方形和正方形 , 点在上,与交于点 , , 正方形的边长为 , 则的长为 .
 10. 如图,反比例函数的图像经过菱形的顶点 , 点在轴上,过点作轴的垂线与反比例函数的图象相交于点.若 , 则点的坐标是.
10. 如图,反比例函数的图像经过菱形的顶点 , 点在轴上,过点作轴的垂线与反比例函数的图象相交于点.若 , 则点的坐标是.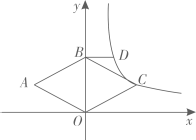 11. 如图,已知点 , 点B在y轴正半轴上,将线段绕点A顺时针旋转到线段 , 若点C的坐标为 , 则 .
11. 如图,已知点 , 点B在y轴正半轴上,将线段绕点A顺时针旋转到线段 , 若点C的坐标为 , 则 . 12. 已知一个菱形的边长是 , 一个内角为 , 则这个菱形的面积是 .13. 如图,∠AOB=60o , 点C在OB上,OC= , P为∠AOB内一点.根据图中尺规作图痕迹推断,点P到OA的距离为 .
12. 已知一个菱形的边长是 , 一个内角为 , 则这个菱形的面积是 .13. 如图,∠AOB=60o , 点C在OB上,OC= , P为∠AOB内一点.根据图中尺规作图痕迹推断,点P到OA的距离为 .
三、解答题
-
14. 如图,在长方形 中,已知 为 上一点, 交 于点 . 若 , 长方形的周长为 , 且 , 求 的长.
 15. 如图,菱形的对角线相交于点为的中点, , .求的长及的值.
15. 如图,菱形的对角线相交于点为的中点, , .求的长及的值.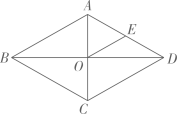
四、计算题
-
16. 计算: .
五、综合题