2023-2024学年初中数学九年级上册 4.1 正弦和余弦 同步分层训练培优卷(湘教版)
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
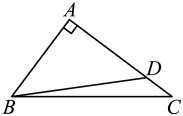
1. 如图,在中, , 若 , , 点是上一点,且 , 则的值为( ).
 A、 B、 C、 D、2. 如图,在中, , , , 则( )
A、 B、 C、 D、2. 如图,在中, , , , 则( )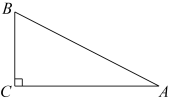 A、 B、 C、4 D、3. 如图,在中, , , , 则的正弦值为( )
A、 B、 C、4 D、3. 如图,在中, , , , 则的正弦值为( ) A、 B、 C、 D、4. 如图,在△ABC中,BC=3,AC=4,∠C=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于AD的长为半径画弧,两弧交于点M、N,作直线MN,分别交AC、AB于点E、F,则AE的长度为( )
A、 B、 C、 D、4. 如图,在△ABC中,BC=3,AC=4,∠C=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于AD的长为半径画弧,两弧交于点M、N,作直线MN,分别交AC、AB于点E、F,则AE的长度为( ) A、 B、3 C、 D、5. 如图,点A在x轴上,点B,C在y轴上,则下列结论正确的是( )
A、 B、3 C、 D、5. 如图,点A在x轴上,点B,C在y轴上,则下列结论正确的是( ) A、 B、 C、 D、6. 如图,点A为边上的任意一点,作于点C,于点D,下列用线段比表示出的值,正确的是( )
A、 B、 C、 D、6. 如图,点A为边上的任意一点,作于点C,于点D,下列用线段比表示出的值,正确的是( ) A、 B、 C、 D、7. 如图,矩形中, , E为的中点,将沿翻折得到 , 延长交于G, , 垂足为H,连接、.以下结论:①; ②; ③;④ , 其中正确的个数是( )
A、 B、 C、 D、7. 如图,矩形中, , E为的中点,将沿翻折得到 , 延长交于G, , 垂足为H,连接、.以下结论:①; ②; ③;④ , 其中正确的个数是( ) A、1 B、2 C、3 D、48. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论,其中正确结论的个数是( )
A、1 B、2 C、3 D、48. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论,其中正确结论的个数是( )①△BDE∽△DPE;②;③;④tan∠DBE=.
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
9. 如图,已知 , 点P、A分别为射线、射线上的动点,将射线绕点P逆时针旋转交射线于点B,则的最大值为.
 10. 将一组完全一样的宽 , 高的多米诺骨牌按图1所示垂直放置在地面上,推动至其全部倒下,最后三块骨牌的位置如图2所示.其中①号骨牌水平倒在地面上,已知②号骨牌与地面夹角的正切值为.
10. 将一组完全一样的宽 , 高的多米诺骨牌按图1所示垂直放置在地面上,推动至其全部倒下,最后三块骨牌的位置如图2所示.其中①号骨牌水平倒在地面上,已知②号骨牌与地面夹角的正切值为. (1)、求的长为cm.(2)、若③号骨牌与地面的夹角的正切值为 , 则的长为cm.11. 将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△EDF中,∠EDF=90°,∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将△EDF绕点D顺时针方向旋转角 , 交AC于点M,交BC于点N,则的值为.
(1)、求的长为cm.(2)、若③号骨牌与地面的夹角的正切值为 , 则的长为cm.11. 将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△EDF中,∠EDF=90°,∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将△EDF绕点D顺时针方向旋转角 , 交AC于点M,交BC于点N,则的值为.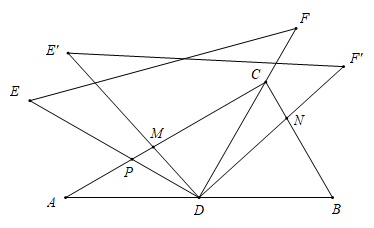 12. 如图,矩形中, , , 是射线上一动点,连结交对角线于点 , 当把分成一个三角形和一个四边形时,这个三角形的面积恰好是面积的 , 则的长为.
12. 如图,矩形中, , , 是射线上一动点,连结交对角线于点 , 当把分成一个三角形和一个四边形时,这个三角形的面积恰好是面积的 , 则的长为. 13. 如图,在边长为4的正方形ABCD内有一动点P,且BP=.连接CP,将线段PC绕点P逆时针旋转90°得到线段PQ.连接CQ、DQ,则DQ+CQ的最小值为 .
13. 如图,在边长为4的正方形ABCD内有一动点P,且BP=.连接CP,将线段PC绕点P逆时针旋转90°得到线段PQ.连接CQ、DQ,则DQ+CQ的最小值为 .
三、解答题
-
14. 已知:如图,在△ABC中,CD⊥AB,sinA = , CD =4,AB =5,求AD的长和tanB的值.
 15. 如图,已知中, , , , 边的垂直平分线分别交、于点D、E.求线段的长.
15. 如图,已知中, , , , 边的垂直平分线分别交、于点D、E.求线段的长.
四、作图题
-
16. 如图,在平面直角坐标系中,的顶点坐标分别为 , , .
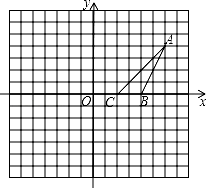 (1)、在y轴左侧,以O为位似中心,画出 , 使它与的相似比为;(2)、根据(1)的作图,.
(1)、在y轴左侧,以O为位似中心,画出 , 使它与的相似比为;(2)、根据(1)的作图,.五、综合题
-
17. 如图,矩形中, , , 点是射线上的动点,点是射线上的动点,满足.
 (1)、若点是的中点,求的长和的值.(2)、若是等腰三角形,求的长.(3)、若 , 点是射线上的点,满足 , 直接写出的长.18. 综合与时间
(1)、若点是的中点,求的长和的值.(2)、若是等腰三角形,求的长.(3)、若 , 点是射线上的点,满足 , 直接写出的长.18. 综合与时间问题情境:如图1,在正方形ABCD中,点E是对角线AC上一点,连接BE,过点E分别作AC,BE的垂线,分别交直线BC,CD于点F,G.试猜想线段BF和CG的数量关系,并加以证明.
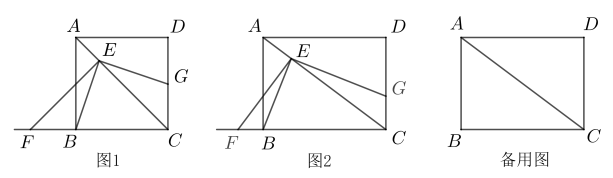 (1)、数学思考:请解答上述问题.(2)、问题解决:如图2,在图1的条件下,将“正方形ABCD”改为“矩形ABCD”,其他条件不变.若 , , 求的值.(3)、问题拓展:在(2)的条件下,当点E为AC的中点时,请直接写出的面积.
(1)、数学思考:请解答上述问题.(2)、问题解决:如图2,在图1的条件下,将“正方形ABCD”改为“矩形ABCD”,其他条件不变.若 , , 求的值.(3)、问题拓展:在(2)的条件下,当点E为AC的中点时,请直接写出的面积.
-