2023-2024学年初中数学九年级上册 4.1 正弦和余弦 同步分层训练基础卷(湘教版)
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 如图,在中, , , , 则的值为( )
 A、 B、 C、 D、2. 如图,在正方形网格中,已知的三个顶点均在格点上,则的正切值为( )
A、 B、 C、 D、2. 如图,在正方形网格中,已知的三个顶点均在格点上,则的正切值为( ) A、2 B、 C、 D、3. 若用我们数学课本上采用的科学计算器计算 , 按键顺序正确的是( )A、
A、2 B、 C、 D、3. 若用我们数学课本上采用的科学计算器计算 , 按键顺序正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 在Rt△ABC中,∠C=90°,cosA= , AB=10,则AC的长为( )A、3 B、4 C、6 D、85. 如图,A、D、B在同一条直线上,电线杆的高度为h,两根拉线与相互垂直, , 则拉线的长度为( )
4. 在Rt△ABC中,∠C=90°,cosA= , AB=10,则AC的长为( )A、3 B、4 C、6 D、85. 如图,A、D、B在同一条直线上,电线杆的高度为h,两根拉线与相互垂直, , 则拉线的长度为( )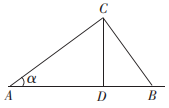 A、 B、 C、 D、6. 如图,在平面直角坐标系中,矩形位置如图放置,点分别在轴上,将逆时针旋转到 , 使得点落在y轴的负半轴上,连接 , 交轴于点.若 , , 则点D的纵坐标是( )
A、 B、 C、 D、6. 如图,在平面直角坐标系中,矩形位置如图放置,点分别在轴上,将逆时针旋转到 , 使得点落在y轴的负半轴上,连接 , 交轴于点.若 , , 则点D的纵坐标是( ) A、2 B、 C、 D、7. 如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,BD与CE相交于O,则图中线段的比不能表示的式子为( )
A、2 B、 C、 D、7. 如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,BD与CE相交于O,则图中线段的比不能表示的式子为( )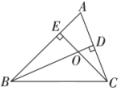 A、 B、 C、 D、8. 如图1,将正方形纸片对折,使与重合,折痕为 . 如图2,展开后再折叠一次,使点C与点E重合,折痕为 , 点B的对应点为点M,交于N,则( )
A、 B、 C、 D、8. 如图1,将正方形纸片对折,使与重合,折痕为 . 如图2,展开后再折叠一次,使点C与点E重合,折痕为 , 点B的对应点为点M,交于N,则( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,在中, , 点D为边的中点,连接 , 若 , 则的值是.
 10. 在Rt△ABC中,∠C=90°,若c=5, ,则AC=.
10. 在Rt△ABC中,∠C=90°,若c=5, ,则AC=. 11. 如图,在一张长方形纸片中, 点 , 分别是和的中点,点是上一点,将矩形的一角沿所在的直线翻折,点恰好落在上,若 , 则的长是.
11. 如图,在一张长方形纸片中, 点 , 分别是和的中点,点是上一点,将矩形的一角沿所在的直线翻折,点恰好落在上,若 , 则的长是. 12. 如图,在中, , .D是边BC的中点,点E在AB边上,将沿直线DE翻折,使点B落在同一平面内点F处,线段FD交边AB于点G,若时,则.
12. 如图,在中, , .D是边BC的中点,点E在AB边上,将沿直线DE翻折,使点B落在同一平面内点F处,线段FD交边AB于点G,若时,则.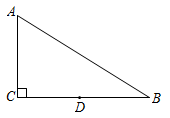 13. 图1是一种折叠式晾衣架展开时的情况,图2是示意图,两个支脚和晾衣臂 , 张开夹角 , 晾衣臂支架.
13. 图1是一种折叠式晾衣架展开时的情况,图2是示意图,两个支脚和晾衣臂 , 张开夹角 , 晾衣臂支架. (1)、当时,的度数为.(2)、当OC从水平方向旋转到时,的面积为.
(1)、当时,的度数为.(2)、当OC从水平方向旋转到时,的面积为.三、解答题
-
14. 为了充分利用四边形余料,小明设计了不同的方案裁剪正方形,裁剪方案与数据如下表:
方案设计
方案1
方案2
裁剪方案示意图


说明
图中的正方形和正方形四个顶点都在原四边形的边上
测量数据
, , , ;
任务1:探寻边角
填空: ▲ , ▲ ;
任务2:比较面积
计算或推理:正方形和正方形边长之比;
任务3:应用实践
若在余料上再截取一个最大正方形,正方形的边长为 ▲ .
15. 如图,矩形ABCD中,M为BC上一点,EM⊥AM交AD的延长线于点E.①求证:△ABM∽△EMA.
②若AB=4,BM=3,求sinE的值.

四、综合题
-
16. 在和中,点在同一直线上,.
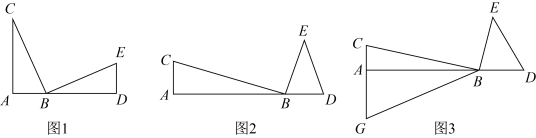 (1)、如图1,如果 , 求证:;(2)、如果 , , .
(1)、如图1,如果 , 求证:;(2)、如果 , , .如图2,当时,求的长;
如图3,点是延长线上一点,且 , 连结 , 如果 , 求的值.
17. 如图1,在菱形中, , , 点E从点A出发以每秒1个单位长度沿运动到点B, 然后以同样速度沿运动到点C停止.设当点E的运动时间为x秒时,长为y.下面是小聪的探究过程,请补充完整.
 (1)、根据三角函数值小聪想到连接交于点O(如图2),请同学们帮忙求的长.(2)、小聪学习了函数知识后,运用函数的研究经验,对y与x的变化规律进行了下列探究,根据点E在上运动到不同位置进行画图、测量,分别得到了y与x的几组对应值,并画出了函数图象(如图3):
(1)、根据三角函数值小聪想到连接交于点O(如图2),请同学们帮忙求的长.(2)、小聪学习了函数知识后,运用函数的研究经验,对y与x的变化规律进行了下列探究,根据点E在上运动到不同位置进行画图、测量,分别得到了y与x的几组对应值,并画出了函数图象(如图3):x
0
1
2
3
4
5
y
5
4.82
4.84
5.06
5.46
6
请同学们继续探究点E在上的运动情况,在同一坐标系中补全图象,并写出这个函数的两条性质.
(3)、结合图象探究发现时,x有四个不同的值.求y取何值时,x有且仅有两个不同的值.