2023-2024学年初中数学九年级上册 3.4 相似图形的判定与性质 同步分层训练培优卷(湘教版)
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 如图,等腰△ABC的周长为16,底边BC= , AB=AC,∠A=36°,线段AB的垂直平分线交AB于点D,交AC于点E,连接BE,则下列说法中错误的是( )
 A、是等腰三角形 B、平分 C、△CBE的周长为 , D、△ABE的周长为:2. 如图,在中, , , 点 , 分别是边 , 上的动点,则的最小值为( )
A、是等腰三角形 B、平分 C、△CBE的周长为 , D、△ABE的周长为:2. 如图,在中, , , 点 , 分别是边 , 上的动点,则的最小值为( ) A、 B、 C、 D、3. 如图,为等边三角形,点 , 分别在边 , 上, , 若 , , 则的长为( )
A、 B、 C、 D、3. 如图,为等边三角形,点 , 分别在边 , 上, , 若 , , 则的长为( ) A、 B、 C、 D、4. 如图,把一个边长为5的菱形沿着直线折叠,使点C与延长线上的点Q重合.交于点F,交延长线于点E.交于点P,于点M, , 则下列结论,① , ② , ③ , ④ . 正确的是( )
A、 B、 C、 D、4. 如图,把一个边长为5的菱形沿着直线折叠,使点C与延长线上的点Q重合.交于点F,交延长线于点E.交于点P,于点M, , 则下列结论,① , ② , ③ , ④ . 正确的是( ) A、①②③ B、②④ C、①③④ D、①②③④5. 如图,在中, , , 、分别为、中点,连接、相交于点 , 点在上,且:: , 则四边形的面积为( )
A、①②③ B、②④ C、①③④ D、①②③④5. 如图,在中, , , 、分别为、中点,连接、相交于点 , 点在上,且:: , 则四边形的面积为( ) A、 B、 C、 D、6. 如图,D、E分别是的边AB、BC上的点,且 , 若 , 则的值为( )
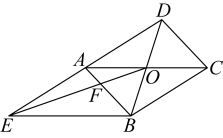
A、 B、 C、 D、6. 如图,D、E分别是的边AB、BC上的点,且 , 若 , 则的值为( ) A、 B、 C、 D、7. 如图,已知F是内的一点, , , 若四边形的面积为2, , , 则的面积是( ).
A、 B、 C、 D、7. 如图,已知F是内的一点, , , 若四边形的面积为2, , , 则的面积是( ). A、6 B、8 C、10 D、128. 如图,在平行四边形ABCD中,E、F分别是边AB、CD的中点,BD分别交CE、AF于G、H,试判断下列结论:①△CBE≌△ADF;②CG=AH;③;④S△CBG=2S△FHD . 其中正确的结论有( )个.
A、6 B、8 C、10 D、128. 如图,在平行四边形ABCD中,E、F分别是边AB、CD的中点,BD分别交CE、AF于G、H,试判断下列结论:①△CBE≌△ADF;②CG=AH;③;④S△CBG=2S△FHD . 其中正确的结论有( )个. A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. 如图,平行四边形的对角线 , 相交于点 , 过点作 , 交的延长线于点E,连接 , 交于点 , 则四边形的面积与的面积的比值为 .
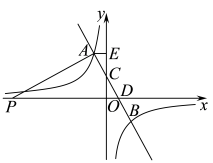
 10. 如图,已知是反比例函数图象上的一点,过点作轴交的图象于点以 , 为边作▱ , 连结交轴于点 , 则 .
10. 如图,已知是反比例函数图象上的一点,过点作轴交的图象于点以 , 为边作▱ , 连结交轴于点 , 则 .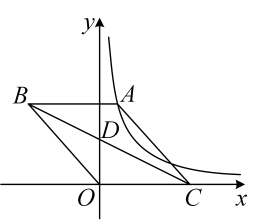 11. 2002年的国际数学家大会在中国北京举行,这是21世纪全世界数学家的第一次大聚会.这次大会的会徽选定了我国古代数学家赵爽用来证明勾股定理的弦图,世人称之为“赵爽弦图”.如图,用四个全等的直角三角形(Rt△AHB≌Rt△BEC≌Rt△CFD≌Rt△DGA)拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH,连接AC和EG,AC与DF、EG、BH分别相交于点P、O、Q,若BE∶EQ=3∶2,则的值是 .
11. 2002年的国际数学家大会在中国北京举行,这是21世纪全世界数学家的第一次大聚会.这次大会的会徽选定了我国古代数学家赵爽用来证明勾股定理的弦图,世人称之为“赵爽弦图”.如图,用四个全等的直角三角形(Rt△AHB≌Rt△BEC≌Rt△CFD≌Rt△DGA)拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH,连接AC和EG,AC与DF、EG、BH分别相交于点P、O、Q,若BE∶EQ=3∶2,则的值是 . 12. 如图,在平面直角坐标系中,四边形 , , , , …都是平行四边形,顶点 , , , , , …都在轴上,顶点 , , , , …都在正比例函数()的图象上,且 , , , …,连接 , , , , …,分别交射线于点 , , , , …,连接 , , , …,得到 , , , ….若 , , , 则的面积为 .
12. 如图,在平面直角坐标系中,四边形 , , , , …都是平行四边形,顶点 , , , , , …都在轴上,顶点 , , , , …都在正比例函数()的图象上,且 , , , …,连接 , , , , …,分别交射线于点 , , , , …,连接 , , , …,得到 , , , ….若 , , , 则的面积为 . 13. 如图,在平面直角坐标系中,正方形的顶点A、C恰好落在双曲线上,且点O在上,交x轴于点E.①当A点坐标为时,D点的坐标为;②当平分时,正方形的面积为 .
13. 如图,在平面直角坐标系中,正方形的顶点A、C恰好落在双曲线上,且点O在上,交x轴于点E.①当A点坐标为时,D点的坐标为;②当平分时,正方形的面积为 .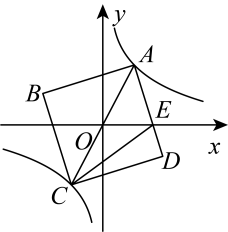
三、解答题
-
14. 如图,为菱形的对角线,点E在的延长线上,且 . 求证: .
 15. 某校九年级一班的兴趣小组准备测量学校外一栋建筑物的高度,出于安全考虑,他们不得离开校园,于是便利用所学知识制定了如下的测量方案:如图所示,首先,王磊站在点 , 并在正前方米的点放置一平面镜,通过平面镜王磊刚好可以看到建筑物的顶端点 , 此时测得王磊的眼睛到地面的距离为米;然后,刘慧在建筑物的影子顶端点竖立了一根高米的标杆 , 此时测得标杆的影子长为米,而王磊与刘慧之间的距离为米,已知 , , , 点 , , , , 在一条直线上,请根据以上数据,计算目标建筑物的高度平面镜大小忽略不计 .
15. 某校九年级一班的兴趣小组准备测量学校外一栋建筑物的高度,出于安全考虑,他们不得离开校园,于是便利用所学知识制定了如下的测量方案:如图所示,首先,王磊站在点 , 并在正前方米的点放置一平面镜,通过平面镜王磊刚好可以看到建筑物的顶端点 , 此时测得王磊的眼睛到地面的距离为米;然后,刘慧在建筑物的影子顶端点竖立了一根高米的标杆 , 此时测得标杆的影子长为米,而王磊与刘慧之间的距离为米,已知 , , , 点 , , , , 在一条直线上,请根据以上数据,计算目标建筑物的高度平面镜大小忽略不计 .
四、综合题