2023-2024学年初中数学九年级上册 3.1 比例线段 同步分层训练培优卷(湘教版)
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 已知是线段的黄金分割点,且 , 则下列比例式能成立的是( )A、 B、 C、 D、2. 某校要举办国庆联欢会,主持人站在舞台中轴线AB的黄金分割点C处(如图1)最自然得体.即 , 在数轴(如题图2)上最接近的点是( )
 A、 B、 C、 D、3. 我国著名数学家华罗庚曾为普及优选法作出重要贡献,优选法中有一种0.618法应用了( )A、黄金分割数 B、平均数 C、众数 D、中位数4. 如图,点D、E分别在△ABC的边AB、AC上,若AD:BD=2:1,点G在DE上,DG:GE=1:2,连接BG并延长交AC于点F , 则AF:EF等于( )
A、 B、 C、 D、3. 我国著名数学家华罗庚曾为普及优选法作出重要贡献,优选法中有一种0.618法应用了( )A、黄金分割数 B、平均数 C、众数 D、中位数4. 如图,点D、E分别在△ABC的边AB、AC上,若AD:BD=2:1,点G在DE上,DG:GE=1:2,连接BG并延长交AC于点F , 则AF:EF等于( )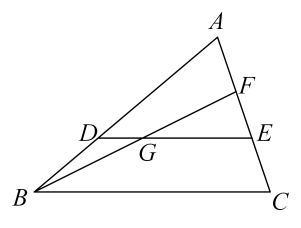 A、1:1 B、4:3 C、3:2 D、2:35. 下列各组数中,成比例的是( ).A、1, , , B、1,4,2, C、5,6,2,3 D、 , , 1,6. 已知非负数 x,y,z 满足. .,设 ,则 W 的最大值与最小值的和为( )A、-2 B、-4 C、-6 D、-87. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )
A、1:1 B、4:3 C、3:2 D、2:35. 下列各组数中,成比例的是( ).A、1, , , B、1,4,2, C、5,6,2,3 D、 , , 1,6. 已知非负数 x,y,z 满足. .,设 ,则 W 的最大值与最小值的和为( )A、-2 B、-4 C、-6 D、-87. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )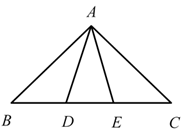 A、 B、 C、 D、8. 设 ,且 ,则 ( )A、673 B、 C、 D、674
A、 B、 C、 D、8. 设 ,且 ,则 ( )A、673 B、 C、 D、674二、填空题
-
9. 已知P点为线段的黄金分割点, , 且 , 则10. 一个比例中,两内项互为倒数,一个外项是3.5,另一个外项是.11. 同学们学习了线段的黄金分割之后,曾老师提出了一个新的定义:点C是线段AB上一点,若=kn,则称点C为线段AB的“近A,n阶黄金分割点”.例如:若=k2 , 则称点C为线段AB的“近A,2阶黄金分割点”;若=k3 , 则称点C为线段AB的“近A,3阶黄金分割点”.若点C为线段AB的“近A,6阶黄金分割点”时,k6= .12. 如图,在黄金矩形ABCD中,四边形ABFG、GHED均为正方形, ,现将矩形ABCD沿AE向上翻折,得四边形 ,连接BB′,若AB=2,则线段 的长度为.
 13. 若 , 则 的值为 .
13. 若 , 则 的值为 .三、解答题
-
14. 已知 , 且 , 求的值。15. 阅读下列解题过程,然后解题:
题目:已知 互不相等),求 的值.
解:设 ,则 , ,
, .
依照上述方法解答下列问题:
已知 ,其中 ,求 的值.
四、综合题
-
16. 定义:如图1,点P为线段AB上一点,如果 =k,那么我们称点P是线段AB的黄金分割点, 叫做黄金分割数.
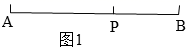
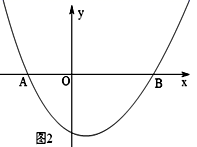 (1)、理解:利用图1,运用一元二次方程的知识,求证:黄金分割数 ;(2)、应用:如图2,抛物线y=x2+nx+2n(n<0)的图象与x轴交于A、B两点(OA<OB),若原点O是线段AB的黄金分割点,①求线段AB的长;②直接写出点A和点B的坐标.
(1)、理解:利用图1,运用一元二次方程的知识,求证:黄金分割数 ;(2)、应用:如图2,抛物线y=x2+nx+2n(n<0)的图象与x轴交于A、B两点(OA<OB),若原点O是线段AB的黄金分割点,①求线段AB的长;②直接写出点A和点B的坐标.