2023-2024学年初中数学九年级上册 2.3 一元二次方程根的判别式 同步分层训练培优卷(湘教版)
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 方程的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、只有一个实数根
-
2. 已知关于的一元二次方程无实数根,则一次函数的图象不经过第( )象限.A、一 B、二 C、三 D、四
-
3. 已知关于x的一元二次方程 , 及函数 , (a,b,c为常数,且),则( )A、若方程有解,则函数的图象一定有交点 B、若方程有解,则函数的图象一定没有交点 C、若方程无解,则函数的图象一定有交点 D、若方程无解,则函数的图象一定没有交点
-
4. 已知是关于x的方程的实数根.下列说法:①此方程有两个不相等的实数根;②当时,一定有;③b是此方程的根;④此方程有两个相等的实数根.上述说法中,正确的有( )A、①② B、②③ C、①③ D、③④
-
5. 关于x的一元二次方程有两个相等的实数根,则( )A、-2 B、2 C、-4 D、4
-
6. 如果关于x的一元二次方程有两个相等的实数根,那么m的值可为( )A、5 B、 C、或3 D、5或
-
7. 已知关于x的一元二次方程(其中p,q为常数)有两个相等的实数根,则下列结论中,错误的是( ).A、1可能是方程的根 B、-1可能是方程的根 C、0可能是方程的根 D、1和-1都是方程的根
-
8. 已知关于x的一元二次方程(其中p,q为常数)有两个相等的实数根,则下列结论中,错误的是( ).A、1可能是方程的根 B、可能是方程的根 C、0可能是方程的根 D、1和-1都是方程的根
二、填空题
-
9. 已知a、b是方程的两根,则 .
-
10. 关于的一元二次方程有两个不相等的实数根,则(写出一个满足条件的值).
-
11. 已知关于x的一元二次方程x2-2x+3m=0有实数根,设此方程的一个实数根为t,令y=t2-2t+4m+1,则y的取值范围为 .
-
12. 已知关于x的一元二次方程(a-3)x2-8x+9=0.(1)、若方程的一个根为x=-1,则a的值为 ;(2)、若方程有实数根,则满足条件的正整数a的值为 .
-
13. 如图是一块矩形菜地ABCD,AB=a(m),AD=b(m),面积为.现将边AB增加1m.
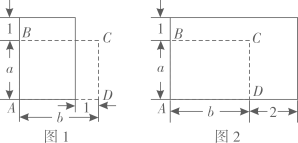 (1)、如图1,若a=5,边AD减少1m,得到的矩形面积不变,则b的值是.(2)、如图2,若边AD增加2m,有且只有一个a的值,使得到的矩形面积为 , 则s的值是.
(1)、如图1,若a=5,边AD减少1m,得到的矩形面积不变,则b的值是.(2)、如图2,若边AD增加2m,有且只有一个a的值,使得到的矩形面积为 , 则s的值是.
三、解答题
-
14. 已知△ABC的三边长分别是a,b,c,其中 , 且关于x的一元二次方程有两个相等的实数根,判断△ABC的形状.
-
15. 已知关于x的一元二次方程有两个相等的实数根,求k的值与方程的根.
四、综合题
-
16. 已知抛物线的顶点在轴上.(1)、求的值;(2)、求的值.
-
17. 对于两个不同的函数,通过加法运算可以得到一个新函数,我们把这个新函数称为两个函数的“和函数”.例如:对于函数和 , 则函数 , 的“和函数”.
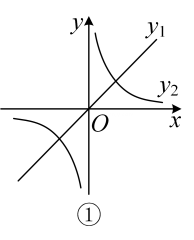 (1)、已知函数和 , 这两个函数的“和函数”记为.
(1)、已知函数和 , 这两个函数的“和函数”记为.①写出的表达式,并求出当x取何值时,的值为;
②函数 , 的图像如图①所示,则的大致图像是 ▲ .
A.
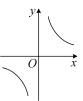 B.
B.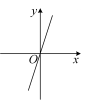 C.
C.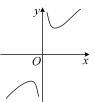 D.
D.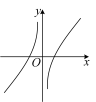 (2)、已知函数和 , 这两个函数的“和函数”记为.
(2)、已知函数和 , 这两个函数的“和函数”记为.①下列关于“和函数”的性质,正确的有 ▲ ;(填写所有正确的选项)
A.的图像与x轴没有公共点
B.的图像关于原点对称
C.在每一个象限内,随x的值增大而减小
D.当时,随着x的值增大,的图像越来越接近的图像
②探究函数与一次函数(为常数,且图像的公共点的个数及对应的k的取值范围,直接写出结论.
