2023-2024学年初中数学九年级上册 2.1 一元二次方程同步分层训练培优卷(湘教版)

试卷更新日期：2023-12-16 类型：同步测试

进入出卷网下载

一、选择题

1. 下列方程为一元二次方程的是（）

A、 $x + 1 = 4$ B、 $x^{2} + y + 1 = 0$ C、 $x^{2} + 3 x = 6$ D、 $x + \frac{1}{x} = 2$

查看试题解析
2. 若关于x的方程（m-3）x^|m^-^1|+5x-3＝0是一元二次方程，则m的值为（　　）

A、3 B、-1 C、3或-1 D、0

查看试题解析
3. 某花圃用花盆培育某种花苗，经过试验发现，每盆花的盈利与每盆株数构成一定的关系，每盆植入3株时，平均单株盈利10元；以同样的栽培条件，若每盆每增加1株，平均单株盈利就减少1元，要使每盆的盈利为40元，需要每盆增加几株花苗？设每盆增加 $x$ 株花苗，下面列出的方程中符合题意的是（）

A、 $(x + 3) (10 + x) = 40$ B、 $(x + 3) (10 - x) = 40$ C、 $(x - 3) (10 + x) = 40$ D、 $(x + 3) (10 + x) = 40$

查看试题解析
4. 为了宣传环保，某学生写了一份倡议书在微博传播，规则为：将倡议书发表在自己的微博，再邀请n个好友转发倡议书，每个好友转发倡议书，又邀请n个互不相同的好友转发倡议书，以此类推，已知经过两轮传播后，共有1641人参与了传播活动，则方程列为（）

A、(n+1)²=1641 B、(n- 1)²=1641 C、n(n+1)=1641 D、1+n+n²=1641

查看试题解析
5. 某商品经过连续两次降价，价格从100元降为64元．已知两次降价的百分率都是x，则x满足的方程是（）

A、64(1-2x)=100 B、100(1-x)²=64 C、64(1-x)²=100 D、100(1-2x)=64

查看试题解析
6. 受电子商务的发展及国家法治环境改善等因素的影响，某公司快递业务量迅猛发展，2020年公司快递业务量为200万件，2022年快递业务量达到288万件，若设快递量平均每年增长率为x，则下列方程中，正确的是（）

A、200(1+2x)=288 B、200(1+x)²=288 C、200(1+x²)=288 D、200(1+2x)²=288

查看试题解析
7. 若关于 $x$ 的方程 $(a - 2) x^{2} - 2 x + 1 = 0$ 是一元二次方程，则（）

A、 $a \neq 2$ B、 $a \neq 0$ C、 $a = 2$ D、 $a = 0$

查看试题解析
8. 将一元二次方程 $3 x^{2} - 8 x = 10$ 化成一般形式后，其中的二次项系数、一次项系数和常数项分别是（）

A、 $- 3 ， 8 ， - 10$ B、 $3 ， - 8 ， 10$ C、 $- 3 ， - 8 ， 10$ D、 $3 ， - 8 ， - 10$

查看试题解析

二、填空题

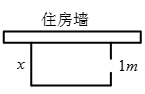
9. 若边长为5的菱形的两条对角线的长分别是关于x的一元二次方程 $x^{2} + (2 m + 1) x + m^{2} - 4 = 0$ 两根的2倍，则m的值为．

查看试题解析
10. 若关于 $x$ 的一元二次方程 $(\begin{array}{l} m - 1 \end{array}) x^{2} + 2 x + m^{2} - 1 = 0$ 的常数项为0，则 $m$ 的值是.

查看试题解析
11. 一花户，有25m长的篱笆，要围成一边靠住房墙（墙长12m）的面积为100m²长方形花园，且垂直于住房墙的一边留一下1m的门，设垂直于住房墙的其中一边长为xm，则可列方程为.

查看试题解析
12. 关于x的方程（1-m²）x²+2mx-1=0的所有根都是比1小的正实数，则实数m的取值范围是．

查看试题解析

三、解答题

13. 若关于x的一元二次方程(m-1) $x^{2}$ +2x+ $m^{2}$ -1=0的常数项为0，求m的值是多少？

查看试题解析
14. 当m为何值时，关于x的方程 $(m - 2) x^{m^{2} - 2} - 4 m x = 0$ 为一元二次方程，并求这个一元二次方程的解．

查看试题解析

四、综合题

15.

(1)、若关于x的方程x²-x-1=mx²（2x-m+1）是一元二次方程，求出它的二次项系数，一次项系数，常数项．

(2)、已知关于x的一元二次方程为2x^m-4xⁿ+（m+n）=0，试直接写出满足要求的所有m、n的值．

查看试题解析
16. 先阅读，再填空解答：
方程 $x^{2} - 3 x - 4 = 0$ 的根为 $x_{1} = - 1 ， x_{2} = 4 ， x_{1} + x_{2} = 3 ， x_{1} x_{2} = - 4$ ；

方程 $3 x^{2} + 10 x + 8 = 0$ 的根为 $x_{1} = - 2 ， x_{2} = - \frac{4}{3} ， x_{1} + x_{2} = - \frac{10}{3} ， x_{1} x_{2} = \frac{8}{3}$ .

(1)、方程 $2 x^{2} + x - 3 = 0$ 的根是x₁= ， x₂= ， $x_{1} + x_{2}$ = ，
$x_{1} x_{2}$ =。

(2)、若 $x_{1} ， x_{2}$ 是关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两个实数根，那么 $x_{1} + x_{2} ， x_{1} x_{2}$ 与系数a、b、c的关系是： $x_{1} + x_{2}$ = ， $x_{1} x_{2}$ =。

(3)、如果 $x_{1} ， x_{2}$ 是方程 $x^{2} + x - 3 = 0$ 的两个根，根据⑵所得的结论，求 $x_{1}^{2} + x_{2}^{2}$ 的值.

查看试题解析

2023-2024学年初中数学九年级上册 2.1 一元二次方程 同步分层训练培优卷(湘教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 2.1 一元二次方程同步分层训练培优卷(湘教版)