2023-2024学年初中数学九年级上册 1.3 反比例函数的应用同步分层训练培优卷(湘教版)

试卷更新日期：2023-12-16 类型：同步测试

进入出卷网下载

一、选择题

1. 图1是一个亮度可调节的台灯，其灯光亮度的改变，可以通过调节总电阻控制电流的变化来实现．图2是该台灯的电流 $I (A)$ 与电阻 $R (Ω)$ 成反比例函数的图象，该图象经过点 $P (880 ， 0.25)$ ．根据图象判断下列说法正确的是（）

A、 $I$ 与 $R$ 的函数关系式是 $I = \frac{200}{R} (R > 0)$ B、当 $R < 880$ 时， $I < 0.25$ C、当 $R > 1000$ 时， $I > 0.22$ D、当 $880 < R < 1000$ 时， $I$ 的取值范围是 $0.22 < I < 0.25$

查看试题解析
2. 如图，点 $A$ 在 $x$ 轴的正半轴上，点 $B ， C$ 在第一象限， $O A ∥ B C ， O C ∥ A B$ ，反比例函数 $y = \frac{1}{x} (x > 0)$ 的图像经过点 $C$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图像经过点 $B$ ．若 $O C = A C$ ，则 $k$ 的值为（）

A、2 B、3 C、4 D、5

查看试题解析
3. 密闭容器内有一定质量的二氧化碳，当容器的体积V（单位： $m^{3}$ ）变化时，气体的密度ρ（单位： $k g / m^{3}$ ）随之变化．已知密度ρ与体积V是反比例函数关系，它的图像如图所示，当 $V = 5 m^{3}$ 时， $ρ = 1.98 k g / m^{3}$ ．根据图像可知，下列说法不正确的是（）

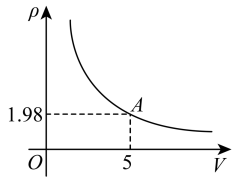A、ρ与V的函数关系式是 $ρ = \frac{9.9}{V} (V > 0)$ B、当 $ρ = 9$ 时， $V = 1.1$ C、当 $V > 5$ 时， $ρ > 1.98$ D、当 $3 < V < 9$ 时，ρ的变化范围是 $1.1 < ρ < 3.3$

查看试题解析
4. 已知闭合电路的电压为定值，电流 $I (A)$ 与电路的电阻 $R (Ω)$ 是反比例函数关系，根据下表判断以下选项正确的是（）
$I$ （A）
5
$⋯$
$a$
$⋯$
$⋯$
$⋯$
$b$
$⋯$
$⋯$
$R$ （Ω）
20
30
40
50
60
70
80
90
100

A、 $I$ 与 $R$ 的关系式为 $I = \frac{R}{100}$ B、 $I$ 与 $R$ 的关系式为 $I = 20 R$ C、 $a < b$ D、当 $2 < I < a$ 时， $40 < R < 50$

查看试题解析
5. 近视眼镜的度数 $y$ （度）与镜片焦距 $x$ （米）之间有如图所示的反比例函数关系，若配制一副度数小于 $400$ 度的近视眼镜，则焦距 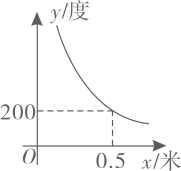$x$ 的取值范围是（）

A、 $0 < x < 0.25$ B、 $x > 0.25$ C、 $0 < x < 1$ D、 $x > 1$

查看试题解析
6. 如图1是一个亮度可调节的台灯，其灯光亮度的改变，可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流 $I (A)$ 与电阻 $R (Ω)$ 成反比例函数的图象，该图象经过点 $P (880 ， 0.25)$ .根据图象可知，下列说法正确的是（）

A、当 $R < 0.25$ 时， $I < 880$ B、I与R的函数关系式是 $I = \frac{200}{R} (R > 0)$ C、当 $R > 1000$ 时， $I > 0.22$ D、当 $880 < R < 1000$ 时，I的取值范围是 $0.22 < I < 0.25$

查看试题解析
7. 一款简易电子秤的工作原理：一个装有踏板（踏板质量忽略不计）的可变电阻 $R_{2}$ ， $R_{2}$ 与踏板人的质量m之间的函数关系式为 $R_{2} = - 2 m + 240 (0 \leq m \leq 120)$ ，其图象如图1所示；图2的电路中，电源电压恒为12伏，定值电阻 $R_{1}$ 的阻值为60欧，接通开关，人站上踏板，电流表显示的读数为I安，该读数可以换算为人的质量m，电流表量程为0~0.2安（温馨提示：导体两端的电压U，导体的电阻R，通过导体的电流I，满足关系式 $I = \frac{U}{R}$ ），则下面结论错误的为（）

A、用含I的代数式表示 $m$ 为 $m = 150 - \frac{6}{I}$ B、电子体重秤可称的最大质量为120千克 C、当 $m = 115$ 时，若电源电压U为12（伏），则定值电阻 $R_{1}$ 最小为70（欧） D、当 $m = 115$ 时，若定值电阻 $R_{1}$ 为40（欧），则电源电压U最大为10（伏）

查看试题解析
8. 如图是反比例函数 $y = \frac{2}{x}$ 和 $y = \frac{a}{x}$ （ $a ＞ 0 ， a$ 为常数）在第一象限内的图象，点M在 $y = \frac{a}{x}$ 的图象上， $M C ⊥ x$ 轴于点C，交 $y = \frac{2}{x}$ 的图象于点A， $M D ⊥ y$ 轴于点D，交 $y = \frac{2}{x}$ 的图象于点B，当点M在 $y = \frac{a}{x}$ 的图象上运动时，以下结论：① $△ O B D$ 与 $△ O C A$ 的面积相等；②四边形 $O A M B$ 的面积不变；③当点A是 $M C$ 的中点时，则点B是 $M D$ 的中点.其中错误结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

9. 如图， $△ A B O$ 中， $A O = 2 A B$ ，点 $C$ 为 $A O$ 中点， $B C$ 的延长线交 $y$ 轴于点 $E$ ， $B E ∥ x$ 轴，过点 $A$ 作 $A D ⊥ B E$ ，垂足为点 $D$ ，反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象经过点 $B$ ，若阴影部分面积为 $4$ ，则 $k$ 的值为．

查看试题解析
10. 为预防传染病，某校定期对教室进行“药熏消毒”.如图所示，药物燃烧阶段，教室内每立方米空气中的含药量 $y (m g)$ 与燃烧时间x（分）成正比例；燃烧后，y与x成反比例.若 $y > 1.6$ ，则x的取值范围是.

查看试题解析
11. 科技小组为了验证某电路的电压 $U (V)$ 、电流 $I (A)$ 电阻 $R (Ω)$ 三者之间的关系： $I = \frac{U}{R}$ ，测得数据如表格：那么，当电阻 $R = 3.6 Ω$ 时，电流 $I =$ A.
$R (Ω)$
2
4
6
9
$I / (A)$
18
9
6
4

查看试题解析
12. 如图，在平面直角坐标系中，一条直线与反比例函数 $y = \frac{8}{x} (x > 0)$ 的图象交于两点A、B，与x轴交于点C，且点B是AC的中点，分别过两点A、B作x轴的平行线，与反比例函数 $y = \frac{2}{x} (x > 0)$ 的图象交于两点D、E，连接DE，则四边形ABED的面积为．

查看试题解析
13. 如图，在平面直角坐标系中，直线 $y = k_{1} x + 4$ 与x轴交于点A，与y轴交于点C，与反比例函数 $y = \frac{k_{2}}{x}$ 在第一象限内的图象交于点B，连接 $B O$ ．若 $S_{△ O B C} = 4 ， t a n ∠ B O C = \frac{1}{4}$ ，则 $k_{2}$ 的值是．

查看试题解析

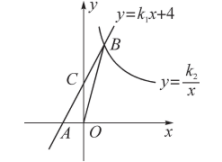
三、解答题

14. 如图，一块砖的A，B，C三个面的面积比是 $4 ： 2 ： 1$ .如果B面向下放在地上，地面所受压强为 $a$ $P a$ ，那么A面和C面分别向下放在地上时，地面所受压强各是多少？

查看试题解析
15. 为了做好校园疫情防控工作，学校后勤每天对全校办公室和教室进行药物喷洒消毒，完成1间教室的药物喷洒要5min ，药物喷洒时教室内空气中的药物浓度 $y$ （单位： ${mg/m}^{3}$ ）与时间 $x$ （单位：min）的函数关系式为 $y = 2 x$ ，其图象为图中线段 $O A$ ，药物喷洒完成后 $y$ 与 $x$ 成反比例函数关系，两个函数图象的交点为 $A (m ， n)$ ，当教室空气中的药物浓度不高于 ${1mg/m}^{3}$ 时，对人体健康无危害，如果后勤人员依次对一班至十一班教室（共11间）进行药物喷洒消毒当最后一间教室药物喷洒完成后，一班能否能让人进入教室？请通过计算说明.

查看试题解析

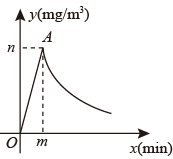
四、综合题

16. 如图1，在平面直角坐标系中，点 $A (- 2 ， 0)$ ，点 $B (0 ， 2)$ ，直线 $A B$ 与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象在第一象限交于点 $C (a ， 4)$ ．

(1)、求反比例函数的解析式

(2)、如图2，点 $E (4 ， m)$ 是反比例函数 $y = \frac{k}{x} (x > 0)$ 图象上一点，连接 $C E$ ， $A E$ 。试问在 $x$ 轴上是否存在一点 $D$ ，使△ACD的面积与△ACE的面积相等，若存在，请求出点 $D$ 的坐标；若不存在，请说明理由。

(3)、在（2）的条件下，坐标原点O关于点 $D$ 的对称点为 $G$ ，且点 $G$ 在 $x$ 轴的正半轴上，若点 $M$ 是反比例函数的第一象限图象上一个动点，连接MG，以MG为边作正方形 $M G N F$ ，当顶点 $F$ 恰好落在直线 $A B$ 上时，求点M的坐标。

查看试题解析
17. 如图，一次函数 $y = k x + b (k > 0)$ 的图象与反比例函数 $y = \frac{8}{x} (x > 0)$ 的图象交于点A，与x轴交于点B，与y轴交于点C， $A D ⊥ x$ 轴于点D， $C B = C D$ ，点C关于直线 $A D$ 的对称点为点E.

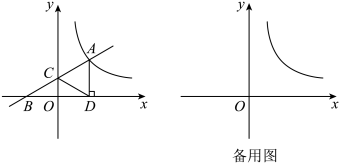(1)、点E是否在这个反比例函数的图象上？请说明理由；

(2)、连接 $A E$ 、 $D E$ ，若四边形 $A C D E$ 为正方形.点P在y轴上，当 $| P E - P B |$ 最大时，求点P的坐标.

查看试题解析

$I$ （A）	5	$⋯$	$a$	$⋯$	$⋯$	$⋯$	$b$	$⋯$	$⋯$
$R$ （Ω）	20	30	40	50	60	70	80	90	100

$R (Ω)$	2	4	6	9
$I / (A)$	18	9	6	4

2023-2024学年初中数学九年级上册 1.3 反比例函数的应用 同步分层训练培优卷(湘教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 1.3 反比例函数的应用同步分层训练培优卷(湘教版)