2023-2024学年初中数学九年级上册 1.2 反比例函数的图像与性质 同步分层训练培优卷(湘教版)
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 已知反比例函数y=(k≠0)与正比例函数y=-2x没有交点,且双曲线图象上有三点A(-1,a)、B(-3,b)、C(4,c),则a、b、c的大小关系为( )A、a>b>c B、b>a>c C、c>b>a D、c>a>b2. 已知反比例函数的图象位于第一、三象限,则m的取值范围是( )A、m>3 B、m>-3 C、m<3 D、m<-33. 对于反比例函数.下列说法不正确的是( )A、图象分布在二,四象限内 B、图象经过点 C、当时,y随x的增大而增大 D、若点都在函数的图象上,且时,则4. 在平面直角坐标系中,已知反比例函数的图象经过 , 则下列说法不正确的是( )A、 B、函数图象位于第一、三象限 C、已知点 , 连接OB,BD,则 D、若 , 则5. 下列图象中是反比例函数图象的是( )A、
 B、
B、 C、
C、 D、
D、 6. 已知、、为双曲线上的三个点,且 , 则以下判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 如图,的三个顶点的坐标分别为 , , , 将绕点顺时针旋转一定角度后使落在轴上,与此同时顶点恰好落在双曲线的图象上,则该反比例函数表达式为( )
6. 已知、、为双曲线上的三个点,且 , 则以下判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 如图,的三个顶点的坐标分别为 , , , 将绕点顺时针旋转一定角度后使落在轴上,与此同时顶点恰好落在双曲线的图象上,则该反比例函数表达式为( ) A、 B、 C、 D、8. 如图,平行四边形的顶点在双曲线上,顶点在双曲线上,中点恰好落在轴上,已知 , 则的值为( )
A、 B、 C、 D、8. 如图,平行四边形的顶点在双曲线上,顶点在双曲线上,中点恰好落在轴上,已知 , 则的值为( ) A、-8 B、-6 C、-4 D、-2
A、-8 B、-6 C、-4 D、-2二、填空题
-
9. 如图,点A在双曲线上,点B在双曲线上,且轴,点C、D在x轴上,若四边形为矩形,则它的面积为
 10. 如图,点A是反比例函数 的图象上的一点,过点A作AB⊥x轴,垂足为B,点C 为y轴上的一点,连接AC、BC,若△ABC的面积为3,则k的值是.
10. 如图,点A是反比例函数 的图象上的一点,过点A作AB⊥x轴,垂足为B,点C 为y轴上的一点,连接AC、BC,若△ABC的面积为3,则k的值是.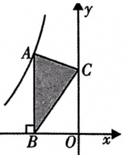 11. 如果点、、是反比例函数图像上的三个点,则、、的大小关系是.(用“”连接)12. 如图,点为直线上的两点,过两点分别作轴的平行线交双曲线于点 , 若 , 则的值为.
11. 如果点、、是反比例函数图像上的三个点,则、、的大小关系是.(用“”连接)12. 如图,点为直线上的两点,过两点分别作轴的平行线交双曲线于点 , 若 , 则的值为. 13. 如图,四边形为矩形,点在第三象限,点关于的对称点为点 , 点 , 都在函数的图象上,轴于点.若的延长线交轴于点 , 当矩形的面积为6时,的值为.
13. 如图,四边形为矩形,点在第三象限,点关于的对称点为点 , 点 , 都在函数的图象上,轴于点.若的延长线交轴于点 , 当矩形的面积为6时,的值为.
三、解答题
-
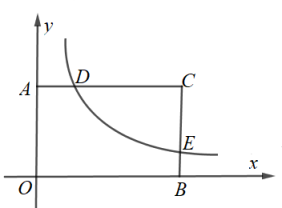
14. 已知反比例函数 的图象位于第二、四象限,正比例函数 图象经过第一、三象限,求k的整数值.15. 如图所示,矩形AOBC的边AO,OB在两坐标轴上,双曲线 与矩形AOBC的边交于点D,E,点C(8,5),求D,E两点的坐标.
四、综合题
-
16. 如图,一次函数y=kx+b与反比例函数y=m/x的图象相交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,已知A点的坐标是(2,3),BC=2.
 (1)、求反比例函数与一次函数的关系式;(2)、点P为反比例函数y=m/x图象上的任意一点,若S_POC=3S_ABC,求点P的坐标.17. 在平面直角坐标系内,已知任意两点的坐标 , 我们把称为A、B两点的“横向距离”,记作=.例如: , 则=.
(1)、求反比例函数与一次函数的关系式;(2)、点P为反比例函数y=m/x图象上的任意一点,若S_POC=3S_ABC,求点P的坐标.17. 在平面直角坐标系内,已知任意两点的坐标 , 我们把称为A、B两点的“横向距离”,记作=.例如: , 则=. (1)、①若点 , 当A、B都在函数的函数图象上时,=.
(1)、①若点 , 当A、B都在函数的函数图象上时,=.②若点 , 当A、B都在函数的函数图象上时,=.
(2)、已知直线交x轴于B点,交y轴于A点,在第一象限内交双曲线于C,D两点,且满足.若恒成立,求m的最大值.(3)、若抛物线与直线在同一坐标平面内交于 , , 且满足下列两个条件:① , ②抛物线过 , 试求的取值范围.