2023-2024学年初中数学九年级上册 1.1 反比例函数同步分层训练培优卷(湘教版)

试卷更新日期：2023-12-16 类型：同步测试

进入出卷网下载

一、选择题

1. 下列函数是反比例函数的是（）

A、 $y = \frac{x}{3}$ B、 $y = \frac{3}{x + 1}$ C、 $y = \frac{x^{2}}{2}$ D、 $y = \frac{3}{x}$

查看试题解析
2. 已知反比例函数 $y = \frac{k}{x} (k \neq 0)$ ，当自变量 $x$ 的值从3增加到6时，函数值减少了1，则函数的表达式为（）

A、 $y = \frac{6}{x}$ B、 $y = \frac{3}{x}$ C、 $y = \frac{2}{x}$ D、 $y = \frac{1}{2 x}$

查看试题解析
3. 已知函数 $y = (m - 2) x^{m^{2} - 5}$ 是反比例函数，则 $m$ 的值为（ )

A、2 B、-2 C、2或-2 D、任意实数

查看试题解析
4. 下列数表中分别给出了变量y与x的几组对应值，其中是反比例函数关系的是（）

A、

$x$

1

2

3

4

$y$

7

8

9

10

B、

$x$

1

2

3

4

$y$

3

6

9

12

C、

$x$

1

2

3

4

$y$

1

0.5

$\frac{1}{3}$

0.25

D、

$x$

1

2

3

4

$y$

4

3

2

1

查看试题解析
5. 购买 $x$ 斤水果需 $24$ 元，购买一斤水果的单价 $y$ 与 $x$ 的关系式是（）

A、 $y = \frac{24}{x} (x > 0)$ B、 $y = \frac{24}{x}$ （ $x$ 为自然数） C、 $y = \frac{24}{x}$ （ $x$ 为整数） D、 $y = \frac{24}{x}$ （ $x$ 为正整数）

查看试题解析
6. 平度高铁通车后极大的方便了市民的出行．平度北站建设初期需要运送大量土石方．某运输公司承担了运送总量为10⁶m³土石方的任务，该运输公司平均每天运送土石方的数量v（单位：m³/天）与完成运送任务所需时间t（单位：天）之间的函数关系式是（）

A、 $v = 10^{6} t$ B、 $v = \frac{10^{6}}{t}$ C、 $v = \frac{t}{10^{6}}$ D、 $v = 10^{6} t^{2}$

查看试题解析
7. 下列各问题中，两个变量之间的关系不是反比例函数的是（）

A、小明完成100m赛跑时，时间t（s）与跑步的平均速度v（m/s）之间的关系. B、菱形的面积为48cm² ，它的两条对角线的长为y（cm）与x（cm）的关系. C、一个玻璃容器的体积为30L时，所盛液体的质量m与所盛液体的体积V之间的关系. D、压力为600N时，压强p与受力面积S之间的关系.

查看试题解析
8. 下列问题中，两个变量成反比例的是（）

A、长方形的周长确定，它的长与宽； B、长方形的长确定，它的周长与宽； C、长方形的面积确定，它的长与宽； D、长方形的长确定，它的面积与宽．

查看试题解析

二、填空题

9. 两位同学在描述同一反比例函数的图象时，甲同学说：“这个反比例函数图象上任意一点到两坐标轴的距离之积是 $12$ ”．乙同学说：“这个反比例函数图象与直线 $y = x$ 有两个交点”．你认为这两个同学所描绘的反比例函数对应的解析式是．

查看试题解析
10. 某商场出倠一批进价为2元的贺卡，在市场营销中发现此商品的日销售单价 $x$ (元)与日销售量 $y$ (个)之间有如下关系：

日销售单价x(元）

3

4

5

6

日销售量y(个）

20

15

12

10

则 $y$ 与 $x$ 之间的函数关系式为.

查看试题解析
11. 在压力不变的情况下，压强是受力面积的反比例函数，当物体的压力F为100牛时，该物体的压强p与受力面积S的函数关系式是.

查看试题解析
12. 函数y＝ $\frac{m + 2}{x^{m^{2} - 3 m - 9}}$ 是反比例函数，则m的值是.

查看试题解析

三、解答题

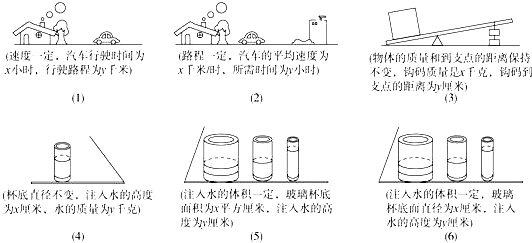
13. 某市为促进经济发展，增强对外贸易的竞争力，把距离港口360千米的普通公路升级成了同等长度的高速公路，结果汽车行驶的平均速度比原来提高了50%，行驶时间缩短了2小时，求汽车原来的平均速度.

查看试题解析
14. 图中，哪些图中的y与x构成反比例关系请指出．

查看试题解析

四、综合题

15. 面积一定的梯形，其上底长是下底长的 $\frac{1}{3}$ ，设上底长为xcm，高为ycm，且当x=5时，y=6.

(1)、求y与x的函数关系式；

(2)、求当y=4时下底的长.

查看试题解析
16. 有600个零件需要在一天内加工完毕，设当工作效率为每人每天加工p个时，需工人q个.

(1)、求q关于p的函数表达式.

(2)、若每人每天的工作效率提高20%，则工人的人数可以减少几分之几?

查看试题解析

$x$	1	2	3	4
$y$	7	8	9	10

$x$	1	2	3	4
$y$	3	6	9	12

$x$	1	2	3	4
$y$	1	0.5	$\frac{1}{3}$	0.25

$x$	1	2	3	4
$y$	4	3	2	1

2023-2024学年初中数学九年级上册 1.1 反比例函数 同步分层训练培优卷(湘教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 1.1 反比例函数同步分层训练培优卷(湘教版)