2023-2024学年初中数学沪科版八年级上册 15.3 等腰三角形同步分层训练基础卷

试卷更新日期：2023-12-16 类型：同步测试

进入出卷网下载

一、选择题

1. $△ A B C$ 为等边三角形，点 D在线段 $B C$ 上，且 $∠ B A D = 20 °$ ，则 $∠ A D C$ 的度数是（）

A、 $40 °$ B、 $60 °$ C、 $80 °$ D、 $100 °$

查看试题解析
2. 下列命题是假命题的是（）.

A、有一个角是60°的等腰三角形是等边三角形 B、有两边和一角对应相等的两个三角形全等 C、平面内垂直于同一直线的两条直线平行 D、全等三角形的面积相等

查看试题解析
3. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D$ 是 $∠ B A C$ 的平分线，若 $B D = 5$ ，则 $C D$ 等于（　　）

A、3 B、4 C、5 D、6

查看试题解析
4. 如图，在 $▱ A B C D$ 中， $A B = 5$ ， $A D = 8$ ， $∠ A B C$ 的平分线 $B E$ 交 $A D$ 于点E，则DE的长是（）

A、4 B、3 C、3.5 D、2

查看试题解析
5. 如图，点A的坐标为 $(1 ， 0)$ ，点B在直线 $y = - x$ 上运动，当线段 $A B$ 最短时，点B的坐标为（）

A、（0，0） B、 $(\frac{1}{2} ， - \frac{1}{2})$ C、 $(\frac{\sqrt{2}}{2} ， - \frac{\sqrt{2}}{2})$ D、 $(- \frac{1}{2} ， - \frac{1}{2})$

查看试题解析
6. 等腰三角形的两条边长分别为5和6，则这个等腰三角形的周长是（）

A、 $11$ 或 $16$ B、 $16$ C、 $17$ D、 $16$ 或 $17$

查看试题解析
7. 若等腰三角形有一个内角为 $110 °$ ，则这个等腰三角形的底角是（）

A、 $70 °$ B、 $45 °$ C、 $35 °$ D、 $50 °$

查看试题解析
8. 如图， $D$ 为 $△ A B C$ 内一点，过点 $D$ 的直线 $E F$ 与边 $A B$ ， $A C$ 分别交于点 $F$ ， $E$ ，若点 $E$ ，点 $F$ 恰好分别在 $C D$ ， $B D$ 的垂直平分线上，记 $∠ D B F = α$ ， $∠ A + 2 ∠ D C E = β$ ，则 $α$ ， $β$ 满足的关系式为（）

A、 $β - α = 90 °$ B、 $β - 2 α = 90 °$ C、 $2 α + β = 180 °$ D、 $2 β + α = 180 °$

查看试题解析

二、填空题

9. 如图①是一把园林剪刀，把它抽象为图②，其中 $O A = O B$ ．若剪刀张开的角为 $40 °$ ，则 $∠ A =$ °．

查看试题解析
10. 如图，在 $△ A B C$ 中， $B C$ 的垂直平分线交 $B C$ 于点D ．交 $A B$ 于点E ．连接 $C E$ ．若 $C E = C A$ ， $∠ A C E = 40 °$ ，则 $∠ B$ 的度数为．

查看试题解析
11. 如图，在等边 $△ A B C$ 中， $D$ ， $E$ 分别为边 $B C$ ， $A B$ 的中点， $A D = 6$ ，且 $P$ 为 $A D$ 上的动点，连接 $E P$ ， $B P$ ，则 $B P + E P$ 的最小值为．

查看试题解析
12. 如图， $A D$ 是 $△ A B C$ 的中线， $∠ A D C = 45 °$ ，把 $△ A D C$ 沿 $A D$ 对折，使点C落在点 $C^{'}$ 的位置，则图中的 $△ B D C^{'}$ 的形状是

查看试题解析
13. 如图， $△ A B C$ 中， $A B = A C$ ， $∠ A = 30 °$ ，射线 $C P$ 从射线 $C A$ 开始绕点C逆时针旋转 $α$ 角 $(0 ° < α < 75 °)$ ，与射线 $A B$ 相交于点D ，将 $△ A C D$ 沿射线 $C P$ 翻折至 $△ A^{'} C D$ 处，射线 $C A^{'}$ 与射线 $A B$ 相交于点E ．若 $△ A^{'} D E$ 是等腰三角形，则 $∠ α$ 的度数为．

查看试题解析

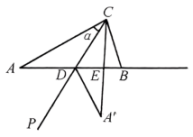
三、解答题

14. 如图，BD平分 $∠ A B C$ ， E是AB上一点，连接DE，使得 $B E = D E$ ． DE与BC平行吗？为什么？

查看试题解析
15. 已知等边 $△ A B C$ 的边长等于4cm，求它的面积是多少？

查看试题解析

四、作图题

16. 如图，已知 $△ A B C$ 中， $A B = A C$ .请用尺规作图法在 $A C$ 边上找一点 $P$ ，使 $△ P A B$ 为等腰三角形.（保留作图痕迹，不写作法）

查看试题解析

五、综合题

17. 如图所示，在等边 $△ A B C$ 中，点 $D$ 是 $B C$ 的中点， $D E ⊥ A B$ 于点 $E$ ，作 $E F ∥ B C$ 交 $A C$ 于点 $F$ ， $B E = 3 c m$ ．

(1)、求证： $△ A E F$ 是等边三角形；

(2)、求 $△ A E F$ 的周长．

查看试题解析
18. 如图，在 $△ A O B$ 中，点 $C$ 为直线 $A B$ 上一动点，以 $O C$ 为直角边在 $A O$ 的同一作等腰直角三角形 $C O D$ ， $∠ D O C = 90 °$ ， $O D = O C$ ．

(1)、特例发现：如图1，如果 $∠ B O A = 90 °$ ， $O A = O B$ ．当点 $C$ 在线段 $A B$ 上时，易证 $△ A O C ≌ △ B O D (S A S)$ ，从而得出结论：线段 $B D$ 与 $A C$ 的数量关系为，位置关系为；

(2)、探究证明：如图2，如果 $∠ B O A = 90 °$ ， $O A = O B$ 条件不变．当点 $C$ 在线段 $A B$ 的延长线上时，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由；

(3)、拓展运用：如图3，若 $△ A O B$ 是锐角三角形， $∠ A B O = 45 °$ ，当点 $C$ 在线段 $A B$ 上运动时，判断线段 $B D$ 与 $A C$ 的位置关系，并说明理由．

查看试题解析

2023-2024学年初中数学沪科版八年级上册 15.3 等腰三角形 同步分层训练基础卷

一、选择题

二、填空题

三、解答题

四、作图题

五、综合题

2023-2024学年初中数学沪科版八年级上册 15.3 等腰三角形同步分层训练基础卷