2023-2024学年初中数学沪科版八年级上册 15.2 线段的垂直平分线 同步分层训练培优卷
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 如图,小红作了如下操作:分别以A,C为圆心,大于长为半径作弧,两弧分别相交于点B,D,依次连接A,B,C,D,则下列说法一定正确的是( )
 A、 B、 C、 D、四边形是正方形2. 如图,在中, , , 分别以点和点为圆心,大于的长为半径画弧,两弧相交于点 , , 作直线 , 交于点 , 连接 , 则的度数为( )
A、 B、 C、 D、四边形是正方形2. 如图,在中, , , 分别以点和点为圆心,大于的长为半径画弧,两弧相交于点 , , 作直线 , 交于点 , 连接 , 则的度数为( ) A、 B、 C、 D、3. 如图,河道l的同侧有M , N两个村庄,计划铺设管道将河水引至M , N两村,下面四个方案中,管道总长度最短的是( )
A、 B、 C、 D、3. 如图,河道l的同侧有M , N两个村庄,计划铺设管道将河水引至M , N两村,下面四个方案中,管道总长度最短的是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,在中, , 为内一点,过点的直线分别交、于点 , , 若在的垂直平分线上,在的垂直平分线上,则的度数为( )
4. 如图,在中, , 为内一点,过点的直线分别交、于点 , , 若在的垂直平分线上,在的垂直平分线上,则的度数为( ) A、 B、 C、 D、5. 如图,直线与x轴,y轴分别交于点A和点B,C,D分别为线段 , 的中点,P为上一动点,当的值最小时,点P的坐标为( )
A、 B、 C、 D、5. 如图,直线与x轴,y轴分别交于点A和点B,C,D分别为线段 , 的中点,P为上一动点,当的值最小时,点P的坐标为( ) A、 B、 C、 D、6. 使用尺规作线段的垂直平分线的痕迹如图所示,下列说法不正确的是( )
A、 B、 C、 D、6. 使用尺规作线段的垂直平分线的痕迹如图所示,下列说法不正确的是( ) A、弧①②的半径长一定相等 B、弧③④的半径长一定相等 C、弧②③的半径长一定相等 D、弧①的半径长大于长度的一半7. 如图,中, , , 是的中线,点、点分别为线段、上的动点,连接、 , 则的最小值为( )
A、弧①②的半径长一定相等 B、弧③④的半径长一定相等 C、弧②③的半径长一定相等 D、弧①的半径长大于长度的一半7. 如图,中, , , 是的中线,点、点分别为线段、上的动点,连接、 , 则的最小值为( ) A、 B、 C、5 D、68. 如图,在R中,∠ABC=90°,以AC为边,作 , 满足AD=AC,E为BC上一点,连接AE,2∠BAE=∠CAD,连接DE.下列结论中正确的有( )
A、 B、 C、5 D、68. 如图,在R中,∠ABC=90°,以AC为边,作 , 满足AD=AC,E为BC上一点,连接AE,2∠BAE=∠CAD,连接DE.下列结论中正确的有( )
①AC⊥DE;②∠ADE=∠ACB;③若CD∥AB,则AE⊥AD;④DE=CE+2BE .
A、①②③ B、②③④ C、②③ D、①②④二、填空题
-
9. 如图,△ABC中,AB的垂直平分线交AC于D,已知AC=10cm,BC=7cm,则△BCD的周长是cm.
 10. 如图,中, , , 的垂直平分线分别交 , 于点 , , 的垂直平分线分别交 , 于点 , , 连接 , 则 .
10. 如图,中, , , 的垂直平分线分别交 , 于点 , , 的垂直平分线分别交 , 于点 , , 连接 , 则 . 11. 如图,在中, , 是的垂直平分线,分别交 , 于点 , . 若 , , 则的周长是 .
11. 如图,在中, , 是的垂直平分线,分别交 , 于点 , . 若 , , 则的周长是 . 12. 如图,在锐角中, , , 的平分线交于点D,点M,N分别是和上的动点,则的最小值是 .
12. 如图,在锐角中, , , 的平分线交于点D,点M,N分别是和上的动点,则的最小值是 .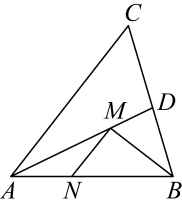 13. 如图,在中, , , , 垂直平分 , 点为直线上的一个动点,则周长的最小值是 。
13. 如图,在中, , , , 垂直平分 , 点为直线上的一个动点,则周长的最小值是 。
三、解答题
-
14. 如图,在中是的垂直平分线, , 的周长为 , 求的周长.
 15. 如图,在中,的垂直平分线交于点E,交于点F,点D为的中点,连接 , 此时 , . 求证: .
15. 如图,在中,的垂直平分线交于点E,交于点F,点D为的中点,连接 , 此时 , . 求证: .
四、综合题
-
16. 如图,直线与坐标轴交于A,B两点,点C坐标为 , 将B点向右平移4个单位,再向下平移1个单位得到点D,直线交直线于点E.
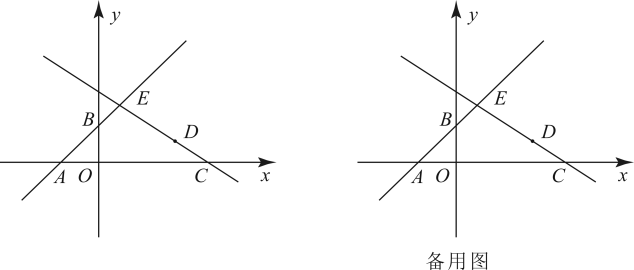 (1)、求直线的表达式;(2)、我们定义:如果一个三角形中有一个内角为 , 则称这个三角形为“天府三角形”
(1)、求直线的表达式;(2)、我们定义:如果一个三角形中有一个内角为 , 则称这个三角形为“天府三角形”①点F是直线上第一象限内一点,若为“天府三角形”,求点F的坐标;
②在①的条件下,当点F的横坐标大于时,作点B关于x轴的对称点 , 点P为直线上的一个动点,连接 , 点Q为线段的中点,连接 , 当最小时,求点Q的坐标.
17. 直线和交于点为常数,且 , 且两直线分别与轴交于两点.
 (1)、试说明的面积为定值.(2)、当的周长最小时,求点的坐标.(3)、当点恰好在轴上时,将直线绕点逆时针旋转后交轴于点 , 求的面积.
(1)、试说明的面积为定值.(2)、当的周长最小时,求点的坐标.(3)、当点恰好在轴上时,将直线绕点逆时针旋转后交轴于点 , 求的面积.