2023-2024学年初中数学沪科版八年级上册 15.2 线段的垂直平分线 同步分层训练基础卷
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 如图,AD是△ ABC的高,AD也是△ABC的中线,则下列结论不一定成立的是( )
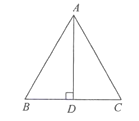 A、AB=AC B、AD=BC C、∠B=∠C D、∠BAD=∠CAD2. 已知:如图,在ΔABC中,AB=AC,AB的垂直平分线DE,分别交AB、AC于点D、E.若AD=3,BC=5,则ΔBEC的周长为( )
A、AB=AC B、AD=BC C、∠B=∠C D、∠BAD=∠CAD2. 已知:如图,在ΔABC中,AB=AC,AB的垂直平分线DE,分别交AB、AC于点D、E.若AD=3,BC=5,则ΔBEC的周长为( ) A、8 B、10 C、11 D、133. 如图,中, , 垂直平分 , 点P为直线上一动点,则的最小值为( )
A、8 B、10 C、11 D、133. 如图,中, , 垂直平分 , 点P为直线上一动点,则的最小值为( ) A、3 B、5 C、6 D、74. 如图,中, , 平分 , , , 则的面积为( )
A、3 B、5 C、6 D、74. 如图,中, , 平分 , , , 则的面积为( ) A、15 B、10 C、15 D、305. 如图,AC=AD,BC=BD,则下列结果正确的是( )
A、15 B、10 C、15 D、305. 如图,AC=AD,BC=BD,则下列结果正确的是( ) A、AB⊥CD B、OA=OB C、∠ACD=∠BDC D、∠ABC=∠CAB6. 如图,△ABC中,AB<AC<BC,如果要使用尺规作图的方法在BC上确定一点P,使PA+PB=BC,那么符合要求的作图痕迹是( )A、
A、AB⊥CD B、OA=OB C、∠ACD=∠BDC D、∠ABC=∠CAB6. 如图,△ABC中,AB<AC<BC,如果要使用尺规作图的方法在BC上确定一点P,使PA+PB=BC,那么符合要求的作图痕迹是( )A、 B、
B、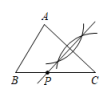 C、
C、 D、
D、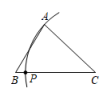 7. 在 中,已知 ,则三角形的形状是( )A、钝角三角形 B、直角三角形 C、锐角三角形 D、无法确定8. 如图,已知 , 用尺规在边上确定一点P,使 . 下面四种作图中,正确的是( )
7. 在 中,已知 ,则三角形的形状是( )A、钝角三角形 B、直角三角形 C、锐角三角形 D、无法确定8. 如图,已知 , 用尺规在边上确定一点P,使 . 下面四种作图中,正确的是( ) A、以B为圆心,为半径画弧,交于点P,点P为所求 B、以C为圆心,为半径画弧,交于点P,点P为所求 C、作的垂直平分线交于点P,点P为所求 D、作的垂直平分线交于点P,点P为所求
A、以B为圆心,为半径画弧,交于点P,点P为所求 B、以C为圆心,为半径画弧,交于点P,点P为所求 C、作的垂直平分线交于点P,点P为所求 D、作的垂直平分线交于点P,点P为所求二、填空题
-
9. 如图,在中,是的垂直平分线,3cm,的周长为12cm,则的周长是.
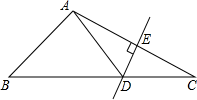 10. 在中,的垂直平分线分别交 , 于点、 , 的垂直平分线分别交 , 于点、 , 若 , , 且的周长为16,求.
10. 在中,的垂直平分线分别交 , 于点、 , 的垂直平分线分别交 , 于点、 , 若 , , 且的周长为16,求. 11. 阅读下面材料:
11. 阅读下面材料:已知: , 依下列步骤尺规作图,并保留作图痕迹.
步骤1:以C为圆心,为半径画弧;
步骤2:以B为圆心,为半径画弧,两弧交于点D;
步骤3:连接 , 交延长线于点E.

下列叙述正确的是 . (填写序号)
①垂直平分线段;②平分;③;④ .
12. 如图,在中,根据尺规作图痕迹,下列四个结论中:①;②;③;④ . 所有正确结论的序号是: . 13. 如图,在锐角三角形中, , , 平分 , 若、分别是、上的动点,则的最小值是 .
13. 如图,在锐角三角形中, , , 平分 , 若、分别是、上的动点,则的最小值是 .
三、解答题
-
14. 如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别是E,F,连接EF,EF与BD相交于点P.求证:EP=FP.
 15. 如图,在中, , 是的垂直平分线,交于点E.已知的周长是24,的长是5.求的周长.
15. 如图,在中, , 是的垂直平分线,交于点E.已知的周长是24,的长是5.求的周长.
四、综合题

