2023-2024学年初中数学沪科版八年级上册 15.1 轴对称图形 同步分层训练培优卷
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 如图所示,图中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在四边形中, , 将四边形沿折叠后,C,D两点分别落在 , 上,若 , 则的大小是( )
2. 如图,在四边形中, , 将四边形沿折叠后,C,D两点分别落在 , 上,若 , 则的大小是( ) A、 B、 C、 D、3. 如图是一正方体的表面展开图.将其折叠成正方体后,与顶点K距离最远的顶点是( )
A、 B、 C、 D、3. 如图是一正方体的表面展开图.将其折叠成正方体后,与顶点K距离最远的顶点是( )
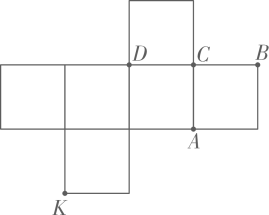 A、A点 B、B点 C、C点 D、D点4. 如图,在△ABC中,已知AB=8,点D、E分别在边AC、AB上,现将△ADE沿直线DE折叠,使点A恰好落在点F处,若将线段BC向左平移刚好可以与线段EF重合,连结CF.若2BC+CF=15,则BC-2CF的值为( )
A、A点 B、B点 C、C点 D、D点4. 如图,在△ABC中,已知AB=8,点D、E分别在边AC、AB上,现将△ADE沿直线DE折叠,使点A恰好落在点F处,若将线段BC向左平移刚好可以与线段EF重合,连结CF.若2BC+CF=15,则BC-2CF的值为( ) A、4 B、5 C、6 D、75. 已知:如图, , 点P在的内部, , 点与点P关于对称,点与点P关于对称,那么以、O、三点为顶点的三角形面积是( )
A、4 B、5 C、6 D、75. 已知:如图, , 点P在的内部, , 点与点P关于对称,点与点P关于对称,那么以、O、三点为顶点的三角形面积是( ) A、4 B、8 C、16 D、无法确定6. 一张长方形纸条按如图所示折叠,是折痕,若 , 则:①;②;③;④ . 以上结论正确的有( )
A、4 B、8 C、16 D、无法确定6. 一张长方形纸条按如图所示折叠,是折痕,若 , 则:①;②;③;④ . 以上结论正确的有( )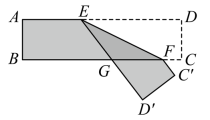 A、①② B、②③④ C、①②③ D、①②③④7. 如图,将一张长方形纸对折两次,则这两条折痕的位置关系是( )
A、①② B、②③④ C、①②③ D、①②③④7. 如图,将一张长方形纸对折两次,则这两条折痕的位置关系是( )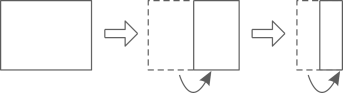 A、平行 B、垂直 C、平行或垂直 D、无法确定8. 如图1,将一条对边互相平行的围巾折叠,并将其抽象成相应的数学模型如图2, , 折痕分别为 , , 若 , , 则等于( )
A、平行 B、垂直 C、平行或垂直 D、无法确定8. 如图1,将一条对边互相平行的围巾折叠,并将其抽象成相应的数学模型如图2, , 折痕分别为 , , 若 , , 则等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,将沿折叠,使点与点重合,若 , , 则 , .
 10. 如图是的正方形网格,要在图中再涂黑一个小正方形,使得图中黑色的部分成为轴对称图形,这样的小正方形有个.
10. 如图是的正方形网格,要在图中再涂黑一个小正方形,使得图中黑色的部分成为轴对称图形,这样的小正方形有个. 11. 如下图,三角形纸片ABC,点D是BC边上一点,连接AD,把沿着AD翻折,得到 , DE与AC交于点F.若点F是DE的中点, , 的面积为9,则点B、E之间的距离为 .
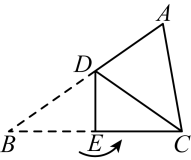
11. 如下图,三角形纸片ABC,点D是BC边上一点,连接AD,把沿着AD翻折,得到 , DE与AC交于点F.若点F是DE的中点, , 的面积为9,则点B、E之间的距离为 . 12. 如图,在三角形ABC中,∠A=56°,∠C=46°,D是线段AC上的一个动点,连接BD,把三角形BCD沿BD折叠,点C落在同一平面内的点C'处,当C′D平行于三角形ABC的边时,∠CDB的大小为 .
12. 如图,在三角形ABC中,∠A=56°,∠C=46°,D是线段AC上的一个动点,连接BD,把三角形BCD沿BD折叠,点C落在同一平面内的点C'处,当C′D平行于三角形ABC的边时,∠CDB的大小为 . 13. 如图,在矩形中, , 点是边上一动点,将沿折叠,使得点落在点处,点分别到的距离分别记为 , 若 , 则的长为
13. 如图,在矩形中, , 点是边上一动点,将沿折叠,使得点落在点处,点分别到的距离分别记为 , 若 , 则的长为
三、解答题
-
14. 如图,长方形纸片 , 点E为边的中点,将纸片沿折叠,点的对应点为 , 连接 . 求证:
 15. 现有5个边长为1的正方形,排列形式如图①,请把它们分割后拼接成一个新的正方形.要求:在图①中画出分割线并在图②正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.
15. 现有5个边长为1的正方形,排列形式如图①,请把它们分割后拼接成一个新的正方形.要求:在图①中画出分割线并在图②正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.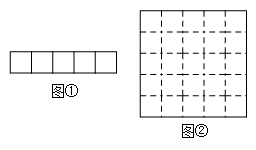
四、综合题
-
16. 如图 , 将笔记本活页一角折过去,使角的顶点落在处,为折痕
 (1)、图中,若 , 求的度数;(2)、如果又将活页的另一角斜折过去,使边与重合,折痕为 , 如图所示, , 求以及的度数;(3)、如果在图中改变的大小,则的位置也随之改变,那么问题中的大小是否改变?请说明理由.17. 探究与运用:
(1)、图中,若 , 求的度数;(2)、如果又将活页的另一角斜折过去,使边与重合,折痕为 , 如图所示, , 求以及的度数;(3)、如果在图中改变的大小,则的位置也随之改变,那么问题中的大小是否改变?请说明理由.17. 探究与运用: (1)、【原题再现】课本第42页有这样一道题:如图1,将纸片沿折叠,使点A落在四边形内点的位置.试探索与之间的数量关系,并说明理由.(2)、【变式探究】如图2,若将原题中“点A落在四边形内点的位置”变为“点A落在四边形外点的位置”,试猜想此时与、之间的数量关系,并说明理由.(3)、【结论运用】
(1)、【原题再现】课本第42页有这样一道题:如图1,将纸片沿折叠,使点A落在四边形内点的位置.试探索与之间的数量关系,并说明理由.(2)、【变式探究】如图2,若将原题中“点A落在四边形内点的位置”变为“点A落在四边形外点的位置”,试猜想此时与、之间的数量关系,并说明理由.(3)、【结论运用】
图1中,连接、 , 若、分别平分 , , 且 , 如图3,则的度数为 .(4)、图2中,连接、 , 若平分 , 平分的外角,若 , , 如图4,则的度数为 .