2023-2024学年初中数学沪科版八年级上册 14.2 全等三角形的判定 同步分层训练培优卷
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 如图,已知BF=DE,AB∥CD,要使△ABF≌△CDE,添加的条件可以是( )
 A、 B、 C、 D、2. 已知下列条件,不能作出三角形的是 ( )A、两边及其夹角 B、两角及其夹边 C、三边 D、两边及除夹角外的另一个角3. 如图, , 增加下列条件可以判定的是( )
A、 B、 C、 D、2. 已知下列条件,不能作出三角形的是 ( )A、两边及其夹角 B、两角及其夹边 C、三边 D、两边及除夹角外的另一个角3. 如图, , 增加下列条件可以判定的是( ) A、 B、 C、 D、4. 如图,和是的高,交于点 , 且 , , 则的长为( )
A、 B、 C、 D、4. 如图,和是的高,交于点 , 且 , , 则的长为( ) A、3 B、4 C、5 D、65. 如图,已知是的中线,E、F分别是和延长线上的点,且 , 连接 , 下列说法中:①;②;③;④ . 正确的是( )
A、3 B、4 C、5 D、65. 如图,已知是的中线,E、F分别是和延长线上的点,且 , 连接 , 下列说法中:①;②;③;④ . 正确的是( )
 A、①②③ B、①②④ C、①③④ D、②③④6. 如图,且且 , 请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
A、①②③ B、①②④ C、①③④ D、②③④6. 如图,且且 , 请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( ) A、50 B、62 C、65 D、687. 如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点(即跷跷板的中点)至地面的距离是 , 当小敏从水平位置下降时,小明离地面的高度是( )
A、50 B、62 C、65 D、687. 如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点(即跷跷板的中点)至地面的距离是 , 当小敏从水平位置下降时,小明离地面的高度是( )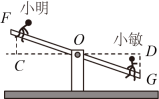 A、 B、 C、 D、8. 如图, , 点在上,且 , 点到射线的距离为 , 点在射线上, . 若的形状,大小是唯一确定的,则的取值范围是( )
A、 B、 C、 D、8. 如图, , 点在上,且 , 点到射线的距离为 , 点在射线上, . 若的形状,大小是唯一确定的,则的取值范围是( ) A、或 B、 C、 D、或
A、或 B、 C、 D、或二、填空题
-
9. 如图,要测量小金河两岸相对的A、两点之间的距离,可以在与垂直的河岸上取、两点,且使 . 从点出发沿与河岸垂直的方向移动到点 , 使点A、、在一条直线上.若测量的长为28米,则A、两点之间的距离为米.
 10. 如图,在中,过点B作的平分线的垂线 . 连接N与中点M,若 , , 则 .
10. 如图,在中,过点B作的平分线的垂线 . 连接N与中点M,若 , , 则 . 11. 如图,在和中,点B , F , C , E在同一直线上, , , 请添加一个条件,使得 . 添加的条件可以是(只需写一个,不添加辅助线);
11. 如图,在和中,点B , F , C , E在同一直线上, , , 请添加一个条件,使得 . 添加的条件可以是(只需写一个,不添加辅助线); 12. 如图,A,B两个建筑物分别位于河的两岸,为了测量它们之间的距离,可以沿河岸作射线 , 且使 , 在上截取 , 过D点作 , 使在一条直线上,测得米,则A,B之间的距离为米.
12. 如图,A,B两个建筑物分别位于河的两岸,为了测量它们之间的距离,可以沿河岸作射线 , 且使 , 在上截取 , 过D点作 , 使在一条直线上,测得米,则A,B之间的距离为米. 13. 如图,已知 , 垂足分别为、 , 、交于点 , 且 , 则图中的全等三角形共有对.
13. 如图,已知 , 垂足分别为、 , 、交于点 , 且 , 则图中的全等三角形共有对.
三、解答题
-
14. 如图,点A , B , D , E在同一条直线上, , , , 请判断与是否相等?并说明你的理由.
 15. 如图,在四边形中, , 点E是的中点, . 求证: .
15. 如图,在四边形中, , 点E是的中点, . 求证: .证明:∵ ,
∴ , ( )
∵ ,
∴
∴∠ ▲ =∠ ▲ .
∵E为中点,
∴
在和中 .
∴( )
∴( )

四、综合题
-
16. 在中,平分交于点D .
 (1)、如图1, , 垂足分别为M , N . 试说明:;(2)、如图2,点E是线段上一点,过点E作交于点F , 与交于点H , 平分交于点G;
(1)、如图1, , 垂足分别为M , N . 试说明:;(2)、如图2,点E是线段上一点,过点E作交于点F , 与交于点H , 平分交于点G;①若 , 则 ▲ ;
②若 , 则 ▲ ;
③探究与之间的数量关系,并说明理由.
17. 如图(1), , , 垂足分别为、 , 点在线段上以的速度由点向点运动,同时点在射线上运动.它们运动的时间为当点运动结束时,点运动随之结束 . (1)、AP , 用含的代数式表示;(2)、若点的运动速度与点的运动速度相等,当时,与是否全等,并判断此时线段和线段的位置关系,请分别说明理由;(3)、如图(2),若“ , ”改为“”,点的运动速度为 , 其它条件不变,当点、运动到何处时有与全等,求出相应的的值.
(1)、AP , 用含的代数式表示;(2)、若点的运动速度与点的运动速度相等,当时,与是否全等,并判断此时线段和线段的位置关系,请分别说明理由;(3)、如图(2),若“ , ”改为“”,点的运动速度为 , 其它条件不变,当点、运动到何处时有与全等,求出相应的的值.