2023-2024学年初中数学沪科版八年级上册 14.2 全等三角形的判定同步分层训练基础卷

试卷更新日期：2023-12-16 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，人字梯中间一般会设计一“拉杆”，这样做的道理是（）

A、三角形具有稳定性 B、垂线段最短 C、两点之间，线段最短 D、两直线平行，内错角相等

查看试题解析
2. 如图，在 $△ A B C$ 和 $△ D E F$ 中，如果 $A B = D E$ ， $B C = E F .$ 在下列条件中不能保证 $△ A B C$ ≌ $△ D E F$ 的是（）

A、 $∠ B = ∠ D E F$ B、 $∠ A = ∠ D$ C、 $A B / / D E$ D、 $A C = D F$

查看试题解析
3. 从数学角度看下列四幅图片有一个与众不同，该图片是（）

A、 B、 C、 D、

查看试题解析
4. 如图，小明书上的三角形被墨迹污染了一部分，他根据所学的知识很快就画了一个与书上完全一样的三角形，那么小明画图的依据是（）

A、 $S S S$ B、 $S A S$ C、 $A A S$ D、 $A S A$

查看试题解析
5. 如图，已知 $∠ D = ∠ A$ ， $∠ 1 = ∠ 2$ ，那么要得到 $△ A B C ≌ △ D E F$ ，还应给出的条件是（）

A、 $∠ E = ∠ B$ B、 $E D = A B$ C、 $E F = A B$ D、 $D F = A B$

查看试题解析
6. 如图，已知 $A B = A C$ ， $A D = A E$ ，欲证 $△ A B D ≌ △ A C E$ ，不可补充的条件是（）

A、 $B D = C E$ B、 $∠ D = ∠ E$ C、 $∠ B A D = ∠ C A E$ D、 $∠ B A C = ∠ D A E$

查看试题解析
7. 小亮设计了如下测量一池塘两端 $A B$ 的距离的方案：先取一个可直接到达点 $A$ ， $B$ 的点 $O$ ，连接 $A O$ ， $B O$ ，延长 $A O$ 至点 $P$ ，延长 $B O$ 至点 $Q$ ，使得 $O P = A O$ ， $O Q = B O$ ，再测出 $P Q$ 的长度，即可知道 $A$ ， $B$ 之间的距离．他设计方案的理由是（）

A、 $S A S$ B、 $A A S$ C、 $A S A$ D、 $S S S$

查看试题解析
8. 小明同学在用直尺和圆规作一个角的平分线，具体过程是这样的：
已知： $∠ A O B$ ．
求作： $∠ A O B$ 的平分线．
作法：第一步：如图，以点 $O$ 为圆心，适当长为半径画弧交 $O A$ 于点 $M$ ，交 $O B$ 于点 $N$ ．
第二步：分别以点 $M 、 N$ 为圆心，大于 $\frac{1}{2}$ 的长为半径画孤，两弧在 $∠ A O B$ 的内部相交于点 $C$ ．
第三步：画射线 $O C$ ．
射线 $O C$ 就是所要求作的 $∠ A O B$ 的平分线．
下列关于小明同学作法的理由，叙述正确的是（）

A、由 $S A S$ 可得 $△ O C M ≌ △ O C N$ ，进而可证 $∠ A O C = ∠ B O C$ B、由 $S S S$ 可得 $△ O C M ≌ △ O C N$ ，进而可证 $∠ A O C = ∠ B O C$ C、由 $A S A$ 可得 $△ O C M ≌ △ O C N$ ，进而可证 $∠ A O C = ∠ B O C$ D、由“等边对等角”可得 $∠ A O C = ∠ B O C$

查看试题解析

二、填空题

9. 如图，有两个长度相同的滑梯靠在一面墙上．已知左边滑梯的高度 $A C$ 与右边滑梯的水平长度 $D F$ 相等，那么判定 $△ A B C$ 与 $△ D E F$ 全等的依据是．

查看试题解析
10. 如图，在Rt $△$ ABC与Rt $△$ DCB中，已知∠A＝∠D＝90°，为了使Rt $△$ ABC≌Rt $△$ DCB，需添加的条件是（不添加字母和辅助线）．

查看试题解析
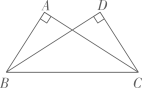11. 如图，把两根钢条的中点连在一起，可以做成一个测量工件内槽的工具（卡钳）．在图中，若测量得 $A^{'} B^{'} = 20 c m$ ，则工件内槽宽 $A B =$ $c m$ ．

查看试题解析
12. 如图，已知 $∠ A C B = ∠ A C D$ ，要用“ $A S A$ ”说明 $△ A B C ≌ △ A D C$ ，则需添加的一个条件是．

查看试题解析

三、解答题

13. 为了测量一幢高楼的高 $A B$ ，在旗杆 $C D$ 与楼之间选定一点 $P$ ．测得旗杆顶 $C$ 的视线 $P C$ 与地面的夹角 $∠ D P C = 17 °$ ，测楼顶 $A$ 的视线 $P A$ 与地面的夹角 $∠ A P B = 73 °$ ，量得点 $P$ 到楼底距离 $P B$ 与旗杆高度相等，等于8米，量得旗杆与楼之间距离为 $D B = 33$ 米，求楼高 $A B$ 是多少米？

查看试题解析
14. 你还记得怎样用尺规作一个角等于已知角吗？小明回顾了作图的过程，并进行了如下的思考，请填出每一步的理由．

由尺规作图知， $O C = O^{'} C^{'}$ ，（），（），

所以 $△ O C D ≌ △ O^{'} C^{'} D^{'}$ （），

所以 $∠ D O C = ∠ D^{'} O^{'} C^{'}$ （）．

查看试题解析

四、综合题

15. 有公共顶点的等腰直角三角形 $A C B$ 与等腰直角三角形 $A D E$ 按如图①所示放置， $∠ B A C = ∠ D A E = 90 °$ ， $A B = A C$ ， $A D = A E$ ，点 $D$ 在 $A C$ 上，点 $E$ 在 $B A$ 的延长线上．连接 $B D$ ， $C E$ ．

(1)、【观察猜想】
$B D$ 与 $C E$ 之间的数量关系是；位置关系是．

(2)、【探究证明】
将等腰直角三角形 $A D E$ 绕点 $A$ 逆时针旋转，如图②所示，使点 $C$ ， $D$ ， $E$ 在同一条直线上，连接 $B D$ ，交 $A C$ 于点 $H$ ． $B D$ 与 $C E$ 之间的关系是否仍然成立？请说明理由

查看试题解析
16. 如图，在平面直角坐标系 $x O y$ 中，四边形 $O A B C$ 的顶点是 $O (0 ， 0)$ ， $A (2 ， 2)$ ， $B (4 ， 2)$ ， $C (4 ， 0)$ ，点P是x轴上一动点，连接 $O B ， A P$ ．

(1)、求直线 $O B$ 的解析式；

(2)、若 $∠ P A O = ∠ A O B$ ，求点P的坐标；

(3)、当点P在线段 $O C$ （点P不与点C重合）上运动时，设 $P A$ 与线段 $O B$ 相交于点D，以 $D A ， D C$ 为边作平行四边形 $A D C E$ ，连接 $B E$ ，求 $B E$ 的最小值．

查看试题解析

2023-2024学年初中数学沪科版八年级上册 14.2 全等三角形的判定 同步分层训练基础卷

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学沪科版八年级上册 14.2 全等三角形的判定同步分层训练基础卷