2023-2024学年初中数学沪科版八年级上册 14.1 全等三角形同步分层训练基础卷

试卷更新日期：2023-12-16 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，AC⊥BE ， DE⊥BE ，若△ABC≌△BDE ， AC=5，DE=2，则CE等于（）

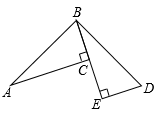A、2.5 B、3 C、3.5 D、4

查看试题解析
2. 如图所示的两个三角形全等，则 $∠ α$ 的度数是（）

A、 $58 °$ B、 $72 °$ C、 $50 °$ D、 $60 °$

查看试题解析
3. 下列说法正确的是（　　）

A、三角形三条角平分线的交点到三角形三个顶点的距离相等 B、等腰三角形的对称轴是它底边上的中线 C、全等三角形的对应边相等 D、两直线平行，同旁内角相等

查看试题解析
4. 两个直角三角形中：①一锐角和斜边对应相等；②斜边和一直角边对应相等；③有两条边相等；④两个锐角对应相等．能使这两个直角三角形全等的是（）

A、①② B、②③ C、③④ D、①②③④

查看试题解析
5. 如图， $△ A B C$ ≌ $△ D E C$ ， $B$ 、 $C$ 、 $D$ 在同一直线上，且 $C E = 5$ ， $A C = 7$ ，则 $B D$ 长（）

A、 $12$ B、 $7$ C、 $2$ D、 $14$

查看试题解析
6. 如图， $△ A B C$ 沿着直线 $B C$ 向右平移得到 $△ D E F$ ， $A C$ 与 $D E$ 相交于点G，则以下四个结论：① $B E = C F$ ；② $A B ∥ D E$ ；③ $D G = E G$ ；④ $S_{四边形 A B E G} = S_{四边形 D G C F}$ ，其中正确的是（　　）

A、①②③ B、①②④ C、②④ D、①③④

查看试题解析
7. 如图，在长方形 $A B C D$ 的中，已知 $A B = 6 c m$ ， $B C = 10 c m$ ，点 $P$ 以 $4 c m / s$ 的速度由点 $B$ 向点 $C$ 运动，同时点 $Q$ 以 $a c m / s$ 的速度由点 $C$ 向点 $D$ 运动，若以 $A$ ， $B$ ， $P$ 为顶点的三角形和以 $P$ ， $C$ ， $Q$ 为顶点的三角形全等，则 $a$ 的值为(　　)

A、 $4$ B、 $6$ C、 $4$ 或 $\frac{9}{2}$ D、 $4$ 或 $\frac{24}{5}$

查看试题解析
8. 如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形 $A B C D$ 、正方形 $E F G H$ 、正方形 $M N P Q$ 的面积分别为 $S_{1} ， S_{2} ， S_{3}$ ．若 $S_{1} + S_{2} + S_{3} = 60$ ，则 $S_{2}$ 的值是（）

A、30 B、20 C、18 D、10

查看试题解析

二、填空题

9. 已知 $△ A B C ≌ △ D E F$ ， $∠ A = 50 °$ ， $∠ F = 40 °$ ，则 $∠ B$ 的度数为．

查看试题解析
10. 如图， $△ A B C ≌ △ D E F$ ，则 $x + y =$ ．

查看试题解析
11. 如图，在平面直角坐标系中，四边形ABCO是正方形，已知点C（ $\sqrt{3}$ ， 1），则点A的坐标是．

查看试题解析
12. 如图，在直角梯形 $A B C D$ 中 $A D ∥ B C$ ， $E$ 是腰 $A B$ 的中点， $C E ⊥ D E$ ， $A D = 5$ ， $B C = 11$ ，则 $D C =$

查看试题解析
13. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 84 °$ ，点 $M$ 为 $A C$ 上一动点，在 $B C$ 上取点 $N$ ，使 $C N = A M$ ，连接 $A N$ ， $B M$ ，当 $A N + B M$ 的值最小时， $∠ A N C$ 的度数为．

查看试题解析

三、解答题

14. 如图，已知 $△ A B C ≌ △ D B E$ ，点D在 $A C$ 上， $B C$ 与 $D E$ 交于点P．若 $∠ A B E = 160 °$ ， $∠ D B C = 30 °$ ，求 $∠ C B E$ 的度数．

查看试题解析
15. 如图，直线 $y = - \frac{4}{3} x + 4$ 与x轴和y轴分别交于A、B两点，把射线AB绕点A顺时针旋转90°得射线AC，点P是射线AC上一个动点，点Q是x轴上一个动点．若 $△ P Q A$ 与 $△ A O B$ 全等，试确定点Q的横坐标．

查看试题解析

四、综合题

16. 如图， $△ A B C ≌ △ D E F$ ，点A对应点D ，点B对应点E ，点B、F、C、E在一条直线上．

(1)、求证： $B F = E C$ ；

(2)、若 $A B = 3$ ， $E F = 7$ ，求 $A C$ 边的取值范围．

查看试题解析
17. 如图，已知直线 $y = \frac{3}{2} x + 3$ 分别交 $x$ 轴， $y$ 轴于A、C两点，直线 $B C$ 过点 $C$ 交 $x$ 轴于点 $B$ ，且 $O C ： O B = 1 ： 2$ ，点D是直线 $A C$ 上的一点且点D的横坐标为 $- 1$ .

(1)、求直线 $B C$ 的解析式；

(2)、已知点P是线段 $B C$ 上的一个动点，点 $Q$ 是 $x$ 轴上的一个动点，当 $△ D P Q$ 是等腰直角三角形时，求点P的坐标.

查看试题解析

2023-2024学年初中数学沪科版八年级上册 14.1 全等三角形 同步分层训练基础卷

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学沪科版八年级上册 14.1 全等三角形同步分层训练基础卷