2023-2024学年初中数学沪科版八年级上册 12.3 一次函数和二次方程同步分层训练基培优卷

试卷更新日期：2023-12-16 类型：同步测试

进入出卷网下载

一、选择题

1. 在同一平面直角坐标系中，直线 $y = 5 x + 3$ 与直线 $y = - 2 x - 3$ 的交点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 已知一次函数 $y = k x + b (k \neq 0)$ 的图象与 $y = - 2 x$ 的图象交于点 $(m ， - 4)$ ．则对于不等式 $\underset{˙}{k} \underset{˙}{x} \underset{˙}{-} \underset{˙}{b} < - 2 x$ ，下列说法正确的是（）

A、当 $k < - 2$ 时， $x > 2$ B、当 $k < - 2$ 时， $x < 2$ C、当 $k > - 2$ 且 $k \neq 0$ 时， $x > - 2$ D、当 $k > - 2$ 且 $k \neq 0$ 时， $x < - 2$

查看试题解析
3. 我国著名数学家华罗庚曾说：“数缺形时少直观，形缺数时难入微”.请用这句话提到的数学思想方法解决下面的问题，已知函数 $y = {\begin{array}{l} x + 1 (x \geq 0) \\ - x - 1 (x < 0) \end{array}$ ，且关于 $x$ ， $y$ 的二元一次方程 $a x - 2 a - y = 0$ 有两组解，则 $a$ 的取值范围是（）

A、 $- \frac{1}{2} \leq a < - \frac{1}{3}$ B、 $- \frac{1}{2} \leq a < \frac{1}{2}$ C、 $- 1 < a \leq - \frac{1}{2}$ D、 $- 1 < a \leq - \frac{1}{3}$

查看试题解析
4. 如图，直线 $y_{1} = x + 3$ 分别与x轴、y轴交于点A和点C，直线 $y_{2} = - x + 3$ 分别与x轴、y轴交于点B和点C，点P（m，2）是△ABC内部（包括边上）一点，则m的最大值与最小值之差为（）

A、1 B、2 C、4 D、6

查看试题解析
5. 如图，一次函数 $y = k x + b$ 与 $y = x + 2$ 的图象相，交于点P(m，4)，则关于x、y的二元一次方程组 ${\begin{array}{l} k x - y = - b \\ y - x = 2 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 2 \\ y = 4 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 4 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = 4 \end{array}$ D ${\begin{array}{l} x = 4 \\ y = 4 \end{array}$

查看试题解析
6. 如图，一次函数 $y = k x + b$ 与 $y = - x + 5$ 的图象的交点坐标为 $(2 ， 3)$ ，则关于x的方程 $- x + 5 = k x + b$ 的解为（）

A、 ${\begin{array}{l} x = 3 \\ x = 2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ x = 3 \end{array}$ C、 $x = 3$ D、 $x = 2$

查看试题解析
7. 一次函数 $y_{1} = k x + b$ （ $k \neq 0$ ， k、b是常数）与 $y_{2} = m x + 3$ （ $m \neq 0$ ， m是常数）的图像交于点 $D (1 ， 2)$ ，下列结论正确的序号是（）
①关于 $x$ 的方程 $k x + b = m x + 3$ 的解为 $x = 1$ ；
②一次函数 $y_{2} = m x + 3$ （ $m \neq 0$ ）图像上任意不同两点 $A (x_{a} ， y_{a})$ 和 $B (x_{b} ， y_{b})$ 满足： $(x_{a} - x_{b}) (y_{a} - y_{b}) < 0$ ；
③若 $| y_{1} - y_{2} | = b - 3$ （ $b > 3$ ），则 $x = 0$ ；
④若 $b < 3$ ，且 $b \neq 2$ ，则当 $x > 1$ 时， $y_{1} > y_{2}$ ．

A、②③④ B、①②④ C、①②③ D、①②③④

查看试题解析

二、填空题

8. 如图，已知函数 $y_{1} = a x + b$ 和 $y_{2} = k x$ 的图象相交于点 $P (- 4 ， - 2)$ ，则不等式 $a x + b < k x$ 的解集是．

查看试题解析
9. 在坐标平面内，已知正比例函数 $y = 2 x$ 与一次函数 $y = x - 1$ 的图象交于点A，则点A的坐标为．

查看试题解析
10. 平行于直线 $y = - 2 x + 3$ ，且与 $y$ 轴交于点 $(0 ， 2)$ 的直线表达式是．

查看试题解析
11. 已知直线 $l_{1} ： y_{1} = k_{1} x + b_{1}$ 与直线 $l_{2} ： y_{2} = k_{2} x + b_{2}$ ，如果满足 $k_{1} = b_{2}$ ， $k_{2} = b_{1}$ ，那么直线 $l_{1}$ 与直线 $l_{2}$ 称为“互为交换直线”如果直线 $y = 2 x + m$ 与其交换直线分别与 $y$ 轴交于点 $A$ 、 $B$ ，且 $A B = 1$ ，那么 $m =$ ．

查看试题解析
12. 将函数 $y = 2 x + b$ （ $b$ 为常数）的图象位于 $x$ 轴下方的部分沿 $x$ 轴翻折至其上方后，所得的折线是函数 $y = | 2 x + b |$ （ $b$ 为常数）的图象．在以下四个结论中正确的是（填序号）．
①当 $b = - 4$ 时，函数 $y = | 2 x + b |$ 的图象与 $x$ 轴的交点是 $(2 ， 0)$ ；
②当 $b = - 4$ 时，函数 $y = | 2 x + b |$ 以的图象与 $y$ 轴的交点是 $(0 ， - 4)$ ；
③不论 $b$ 为任意常数，函数 $y = | 2 x + b |$ 的最小值都是0；
④若 $y = | 2 x + b |$ 图象在直线 $y = 2$ 下方的点的横坐标 $x$ 满足 $0 < x < 3$ ，则 $b$ 的取值范围为 $- 4 \leq b \leq - 2$ ．

查看试题解析

三、解答题

13. 已知直线 $y = k x + b$ 与直线 $y = 2 x + 6$ 交于点A，点A的横坐标为4，且直线 $y = k x + b$ 经过点 $B (- 2 ， 0)$ ，求k，b的值．

查看试题解析
14. 如图所示，直线 $l_{1}$ ， $l_{2}$ 相交于A点，请根据图象求出直线 $l_{1}$ ， $l_{2}$ 的解析式，并直接写出以交点A的坐标为解的二元一次方程组的解．

查看试题解析

四、作图题

15. 阅读与思考：在函数的学习过程中，我们利用描点法画出函数的图象，并借助图象研究该函数的性质，最后运用函数解决问题．现我们对函数y=|x-1|（x的取值范围为任意实数）进行探究．

x	…	$- 3$	$- 2$	$- 1$	0	1	2	3	…
y=\|x-1\|	…	4	▲	2	1	0	▲	2	…

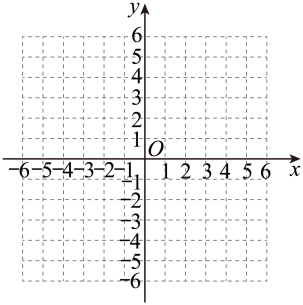
⑴请将上面的表格补充完整．

⑵请根据上表中的数据，在如图所示的平面直角坐标系中画出这个函数的图象，并回答：当 $x > 1$ 时，y的值随x值的增大而 ▲ ．

⑶请在如图所示的平面直角坐标系中画出正比例函数 $y = x$ 的图象，并直接写出不等式 $x < | x - 1 |$ 的解集．

查看试题解析

五、综合题

16. 学校计划为“用英语讲中国故事”演讲比赛购买奖品，已知购买4个A奖品和3个B奖品共需165元；购买6个A奖品和2个B奖品共需210元．

(1)、求A，B两种奖品的单价；

(2)、学校准备购买A，B两种奖品共20个，且A奖品的数量不少于B奖品数量的 $\frac{2}{5}$ ，请设计出最省钱的购买方案，并说明理由．

查看试题解析
17. 已知直线 $y = k x + b$ 经过点 $A (8 ， 0)$ ， $B (4 ， 4)$ ．

(1)、求直线 $A B$ 的解析式；

(2)、若直线 $y = x - 2$ 与直线 $A B$ 相交于点C，求点C的坐标；

(3)、根据图象，写出关于x的不等式 $x > k x + b + 2$ 的解集．

查看试题解析