2023-2024学年初中数学沪科版八年级上册 12.3 一次函数和二次方程 同步分层训练基础卷
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 如图,函数和的图象交于点 , 则不等式的解集为( )
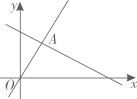 A、 B、 C、 D、2. 如图,在平面直角坐标系中,一次函数(a、b为常数,且)的图象与一次函数的图象相交于点P,若点P的纵坐标为8,则关于x,y的方程组的解是( )
A、 B、 C、 D、2. 如图,在平面直角坐标系中,一次函数(a、b为常数,且)的图象与一次函数的图象相交于点P,若点P的纵坐标为8,则关于x,y的方程组的解是( )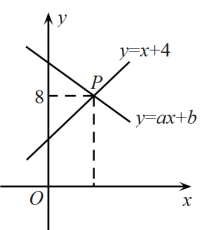 A、 B、 C、 D、3. 如图,直线分别与轴、轴交于点和点 , 直线分别与轴、轴交于点和点 , 点是内部(包括边上)的一点,则的最大值与最小值之差为( )
A、 B、 C、 D、3. 如图,直线分别与轴、轴交于点和点 , 直线分别与轴、轴交于点和点 , 点是内部(包括边上)的一点,则的最大值与最小值之差为( ) A、1 B、2 C、4 D、64. 已知二元一次方程组 的解为 ,则函数 和 的图象交点坐标为( )A、(3,-1) B、(-3,1) C、(1,-3) D、(-1,3)5. 在同一平面直角坐标系中,若一次函数与图象交于点M , 则点M的坐标为( )A、 B、 C、 D、6. 已知甲、乙两弹簧的长度y(cm)与所挂物体x(kg)之间的函数解析式分别是y1=k1x+b1 , y2=k2x+b2 , 图象如图所示,当所挂物体质量均为2kg时,甲、乙两弹簧的长度y1与y2的大小关系为
A、1 B、2 C、4 D、64. 已知二元一次方程组 的解为 ,则函数 和 的图象交点坐标为( )A、(3,-1) B、(-3,1) C、(1,-3) D、(-1,3)5. 在同一平面直角坐标系中,若一次函数与图象交于点M , 则点M的坐标为( )A、 B、 C、 D、6. 已知甲、乙两弹簧的长度y(cm)与所挂物体x(kg)之间的函数解析式分别是y1=k1x+b1 , y2=k2x+b2 , 图象如图所示,当所挂物体质量均为2kg时,甲、乙两弹簧的长度y1与y2的大小关系为 A、y1>y2 B、y1=y2 C、y1<y2 D、不能确定7. 直线与直线平行,且与y轴交于点 , 则其函数表达式是( )A、 B、 C、 D、8. 若一次函数与的交点坐标为 , 如图所示,则的解集为( )
A、y1>y2 B、y1=y2 C、y1<y2 D、不能确定7. 直线与直线平行,且与y轴交于点 , 则其函数表达式是( )A、 B、 C、 D、8. 若一次函数与的交点坐标为 , 如图所示,则的解集为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 已知直线经过点 , 并且与直线平行,那么 .10. 如图,已知函数与函数的图象交于点 , 则方程组的解是 .
 11. 如图,直线y₁=x+b与y₂=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是.
11. 如图,直线y₁=x+b与y₂=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是. 12. 已知一个函数的图象是一条经过原点且与一次函数的图象平行的直线,这个函数的表达式是 .13. 如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4),点P是对角线OB上一个动点,点D的坐标为(0,﹣2),当DP与AP之和最小时,点P的坐标为
12. 已知一个函数的图象是一条经过原点且与一次函数的图象平行的直线,这个函数的表达式是 .13. 如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4),点P是对角线OB上一个动点,点D的坐标为(0,﹣2),当DP与AP之和最小时,点P的坐标为
三、解答题
