2023-2024学年初中数学沪科版八年级上册 12.2 一次函数 同步分层训练培优卷
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 一次函数y=-4x+8图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知点 , 在正比例函数的图象上,且当时,有 , 则的取值范围是( )A、 B、 C、 D、3. 已知一次函数的函数值随的增大而减小,则该函数的图象大致是( )A、
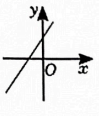 B、
B、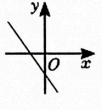 C、
C、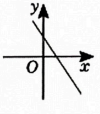 D、
D、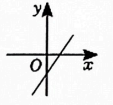 4. 关于函数 , 下列结论中正确的是( )A、函数图象经过点 B、函数图象经过第一、二、四象限 C、函数图象与轴的交点为 D、不论取何值,总有5. 如图所示,已知直线经过点和点 , 直线经过点 , 则关于的不等式的解集是( )
4. 关于函数 , 下列结论中正确的是( )A、函数图象经过点 B、函数图象经过第一、二、四象限 C、函数图象与轴的交点为 D、不论取何值,总有5. 如图所示,已知直线经过点和点 , 直线经过点 , 则关于的不等式的解集是( ) A、 B、 C、 D、6. 如图,一次函数与的图象交于点 , 则关于的不等式的解集为( )
A、 B、 C、 D、6. 如图,一次函数与的图象交于点 , 则关于的不等式的解集为( ) A、 B、 C、 D、7. 把直线向上平移后得到直线 , 若直线经过点 , 且 , 则直线的表达式为( )A、 B、 C、 D、8. 如图,一次函数与的图象的交点坐标为 , 则关于x的方程的解为( )
A、 B、 C、 D、7. 把直线向上平移后得到直线 , 若直线经过点 , 且 , 则直线的表达式为( )A、 B、 C、 D、8. 如图,一次函数与的图象的交点坐标为 , 则关于x的方程的解为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
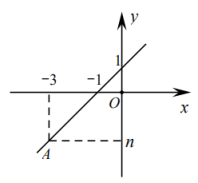
9. 若点 , 在直线上,且满足 , 则(选填“>”或“<”).10. 个月的婴儿生长发育非常快,他们的体重(克)与月龄(月)之间的关系可以用来近似地表示,其中是婴儿出生时的体重.某个婴儿出生时的体重是3800克,月龄时体重是7000克.11. 如图,一次函数( , 是常数,)的图象如图所示,请你写出一个的值 , 使得不等式成立.
 12. 将函数(为常数)的图象位于轴下方的部分沿轴翻折至其上方后,所得的折线是函数(为常数)的图象.在以下四个结论中正确的是(填序号).
12. 将函数(为常数)的图象位于轴下方的部分沿轴翻折至其上方后,所得的折线是函数(为常数)的图象.在以下四个结论中正确的是(填序号).①当时,函数的图象与轴的交点是;
②当时,函数以的图象与轴的交点是;
③不论为任意常数,函数的最小值都是0;
④若图象在直线下方的点的横坐标满足 , 则的取值范围为 .
13. 在平面直角坐标系中,已知一次函数的图象与轴交于 , 与轴交于点.点是直线上的一个动点,将点向下平移4个单位长度得到点 , 若线段与轴有一个公共点,设点的横坐标为 , 则的取值范围是 .三、解答题
-
14. 已知一次函数的图象经过点与 , 求这个一次函数的解析式.15. 已知,直线y=kx+b与直线相交于点 , 与轴、轴分别交于点A、B,点的坐标为.求直线的函数解析式及点的坐标.

四、作图题
-
16. 阅读与思考:在函数的学习过程中,我们利用描点法画出函数的图象,并借助图象研究该函数的性质,最后运用函数解决问题.现我们对函数y=|x-1|(x的取值范围为任意实数)进行探究.
x
…
0
1
2
3
…
y=|x-1|
…
4
▲
2
1
0
▲
2
…
⑴请将上面的表格补充完整.
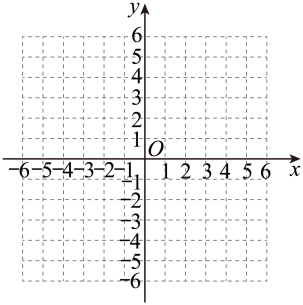
⑵请根据上表中的数据,在如图所示的平面直角坐标系中画出这个函数的图象,并回答:当时,y的值随x值的增大而 ▲ .
⑶请在如图所示的平面直角坐标系中画出正比例函数的图象,并直接写出不等式的解集.
五、综合题


