2023-2024学年初中数学沪科版八年级上册 11.2 图形在坐标系中的平移同步分层训练培优卷

试卷更新日期：2023-12-16 类型：同步测试

进入出卷网下载

一、选择题

1. 平面直角坐标系中一点 $A (- 1 ， 2)$ ，点A关于y轴对称的点坐标是（）

A、 $(- 1 ， - 2)$ B、 $(1 ， 2)$ C、 $(1 ， - 2)$ D、 $(2 ， 1)$

查看试题解析
2. 如图，在平面直角坐标系中，△ABC位于第二象限，点A的坐标是（-2，3），先把△ABC向右平移4个单位长度得到△A₁B₁C₁ ，再作与△A₁B₁C₁关于x轴对称的△A₂B₂C₂ ，则点A的对应点A₂的坐标是（）

A、(-3，2) B、（2，-3） C、（1，-2） D、（-1，2）

查看试题解析
3. 已知平面直角坐标系内某图形各点的横坐标不变，纵坐标都乘以-1，则所得到的图形于原图形的关系是（）

A、关于x轴对称 B、关于y轴对称 C、关于直线x=-1对称 D、关于直线y=-1对称

查看试题解析
4. 点 $A (a - 8 ， 3)$ ，点 $B (2 ， b + 3)$ 关于 $x$ 轴对称，则 $a + b$ 的平方根为（）

A、1 B、2 C、 $\pm 2$ D、 $\pm 1$

查看试题解析
5. 如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到△DEF的位置，AB＝8，DO＝3，平移距离为4，则阴影部分的面积为（）

A、18 B、24 C、26 D、32

查看试题解析
6. 在平面直角坐标系 $x O y$ 中，线段 $A B$ 的两个端点坐标分别为 $A (- 1 ， - 1)$ ， $B (1 ， 2)$ ，平移线段 $A B$ ，平移后其中一个端点的坐标为 $(3 ， - 1)$ ，则另一端点的坐标为（）

A、 $(1 ， 4)$ B、 $(5 ， 2)$ C、 $(1 ， - 4)$ 或 $(5 ， 2)$ D、 $(- 5 ， 2)$ 或 $(1 ， - 4)$

查看试题解析
7. 在如图所示的平面直角坐标系内，画在透明胶片上的平行四边形ABCD，点A的坐标是（0，2）．现将这张胶片平移，使点A落在点A′（4，﹣2）处，则此平移可以是（）．

A、先向右平移5个单位，再向下平移1个单位 B、先向右平移5个单位，再向下平移3个单位 C、先向右平移4个单位，再向下平移4个单位 D、先向右平移4个单位，再向下平移3个单位

查看试题解析
8. 如图，△AOB关于x轴对称图形△A′OB，若△AOB内任意一点P的坐标是（a，b），则△A′OB中的对应点Q的坐标是（　　）

A、（a，b） B、（﹣a，b） C、（﹣a，﹣b） D、（a，﹣b）

查看试题解析

二、填空题

9. 在平面直角坐标系中，点A的坐标为（-4，3）．若线段AB∥y轴，且AB的长为6，则点B的坐标为．

查看试题解析
10. 如图，在平面直角坐标系中， $△ O A B$ 的顶点 $A$ ， $B$ 的坐标分别为 $(3 ， \sqrt{3})$ ， $(4 ， 0)$ ，把 $△ O A B$ 沿 $x$ 轴向右平移得到 $△ C D E$ ，如果点 $D$ 的坐标为 $(6 ， \sqrt{3})$ ，则点 $E$ 的坐标为．

查看试题解析
11. 在平面直角坐标系xOy中，将一个横、纵坐标都是整数的点，沿平行（或垂直）于坐标轴的直线平移1个单位长度，称为该点走了1步．点 $A (1 ， 0)$ ， $B (2 ， 4)$ ， $C (3 ， 1)$ 各走了若干步后到达同一点P，当点P的坐标为时，三个点的步数和最小，为．

查看试题解析
12. 如图：在直角坐标系中，设一动点自 $P_{0} (1 ， 0)$ 处向上运动1个单位至 $P_{1} (1 ， 1)$ ，然后向左运动2个单位至 $P_{2}$ 处，再向下运动3个单位至 $P_{3}$ 处，再向右运动4个单位至 $P_{4}$ 处，再向上运动5个单位至 $P_{5}$ 处，如此继续运动下去．设 $P_{n} (x_{n} ， y_{n})$ ， $n = 1$ ， 2，3…，则 $x_{1} + x_{2} + x_{3} + \cdot \cdot \cdot + x_{2020} + x_{2021} + x_{2022} =$ ．

查看试题解析

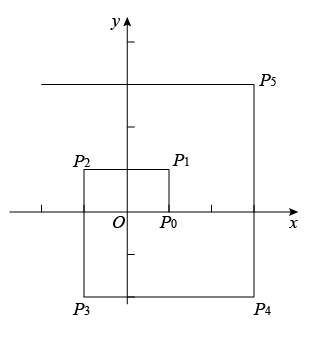
三、解答题

13. 在直角坐标系中，已知A（1，5），B（﹣4，﹣2），C（1，0）三点．

(1)、点A关于x轴的对称的A′的坐标为；点B关于y轴的对称点B′的坐标为；点C关于y轴的对称点C′的坐标为．

(2)、求（1）中的△A′B′C′的面积．

查看试题解析
14. 某宾馆重新装修后，准备在大厅的楼梯上铺设一种红地毯，已知这种地毯每平方米售价70元，楼梯宽2米，楼梯侧面及相关数据如图所示，求买地毯至少需要多少元？

查看试题解析

四、作图题

15. 综合与实践
操作发现

如图，在平面直角坐标系中，已知线段 $A B$ 两端点的坐标分别为 $A (2 ， 6)$ ， $B (5 ， 2)$ ，点 $M$ 的坐标为 $(- 3 ， 6)$ ，将线段 $A B$ 沿 $A M$ 方向平移，平移的距离为 $A M$ 的长度.

(1)、画出 $A B$ 平移后的线段 $M N$ ，直接写出点 $B$ 对应点 $N$ 的坐标；

(2)、连接 $M A$ ， $N B$ ， $A N$ ，已知 $A N$ 平分 $∠ M A B$ ，求证： $∠ M N A = ∠ B N A$ ；
拓展探索

(3)、若点 $P$ 为线段 $A B$ 上一动点（不含端点），连接 $P M$ ， $P N$ ，试猜想 $∠ A M P$ ， $∠ M P N$ 和 $∠ B N P$ 之间的关系，并说明理由.

查看试题解析

五、综合题

16. 已知点 $A (3 x - 5 ， 6 - 2 x)$ ， B点坐标为 $(1 ， - 2)$ ．

(1)、若点A和点B关于x轴对称，求A点坐标；

(2)、若直线 $A B ∥ x$ 轴，求A点坐标．

查看试题解析
17. 对于平面直角坐标系 $x O y$ 中的不同两点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ，给出如下定义：若 $x_{1} x_{2} = 1$ ， $y_{1} y_{2} = 1$ ，则称点 $A$ ， $B$ 互为“倒数点”，例如：点 $A (\frac{1}{2} ， 1)$ ， $B (2 ， 1)$ 互为“倒数点”．

(1)、已知点A的坐标为 $(1 ， 3)$ ，则点A的“倒数点”点B的坐标为；将线段 $A B$ 向右平移2个单位得到线段 $A^{'} B^{'}$ ，则线段 $A^{'} B^{'}$ 上（填“存在”或“不存在”）“倒数点”．

(2)、如图，在正方形 $C D E F$ 中，点C坐标为 $(\frac{1}{2} ， \frac{1}{2})$ ，点D坐标为 $(\frac{3}{2} ， \frac{1}{2})$ ，请判断该正方形的边上是否存在“倒数点”，并说明理由．

查看试题解析

2023-2024学年初中数学沪科版八年级上册 11.2 图形在坐标系中的平移 同步分层训练培优卷

一、选择题

二、填空题

三、解答题

四、作图题

五、综合题

2023-2024学年初中数学沪科版八年级上册 11.2 图形在坐标系中的平移同步分层训练培优卷