2023-2024学年初中数学沪科版八年级上册 11.1 平面内点的坐标同步分层训练培优卷

试卷更新日期：2023-12-16 类型：同步测试

进入出卷网下载

一、选择题

1. 青岛火车站是一座百年老站，是青岛市的标志性建筑之一．下列能准确表示青岛火车站地理位置的是（）

A、山东省青岛市 B、青岛市市南区泰安路2号 C、栈桥风景区的西北方向 D、胶州湾隧道口大约2千米处

查看试题解析
2. 有甲、乙、丙三人，它们所在的位置不同，他们三人都以相同的单位长度建立不同的平面直角坐标系，甲说：“如果以我为坐标原点，乙的位置是(4，3)．”丙说：“如果以我为坐标原点，乙的位置是(-3，-4)．”如果以乙为坐标原点，那么甲和丙的位置分别是（）

A、(3，4)，(-3，-4) B、(4，-3)，(3，-4) C、(-3，-4)，(4，3) D、(-4，-3)，(3，4)

查看试题解析
3. 在平面直角坐标系中，点P(1，- $\sqrt{2}$ )到x轴的距离为（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、3

查看试题解析
4. 在平面直角坐标系中，有一点 $A (n - 1 ， m + 3)$ 在第一象限，且点A到x轴的距离为2，到y轴的距离为4，则n、m的值分别为（）

A、5， $- 1$ B、3，1 C、2，4 D、4，2

查看试题解析
5. 如图，在平面直角坐标系xOy中，已知点A的坐标是（0，2），以OA为边在右侧作等边三角形OAA₁ ，过点A₁作x轴的垂线，垂足为点O₁ ，以O₁A₁为边在右侧作等边三角形O₁A₁A₂ ，再过点A₂作x轴的垂线，垂足为点O₂ ，以O₂A₂为边在右侧作等边三角形O₂A₂A₃ ， …，按此规律继续作下去，得到等边三角形O₂₀₂₂A₂₀₂₂A₂₀₂₃ ，则点A₂₀₂₃的纵坐标为（）

A、（ $\frac{1}{2}$ ）²⁰²¹ B、（ $\frac{1}{2}$ ）²⁰²² C、（ $\frac{1}{2}$ ）²⁰²³ D、（ $\frac{1}{2}$ ）²⁰²⁴

查看试题解析
6. 在平面直角坐标系中，点A的坐标为 $(- 1 ， 3)$ ，点B的坐标为（4，3），则线段AB上任意一点的坐标可表示为（）

A、 $(x ， 3) (- 1 \leq x \leq 4)$ B、 $(x ， 3) (x \leq 4)$ C、 $(x ， 3) (x \geq - 1)$ D、 $(x ， 3)$

查看试题解析
7. 直角坐标系中，我们定义横、纵坐标均为整数的点为整点在0<x<3内，直线y=x+2和y=-x所围成的区域中，整点一共有（）

A、8个 B、7个 C、6个 D、5个

查看试题解析
8. 如图，在平面直角坐标系中，长方形ABCD的顶点坐标分别为A(-1，2)，B(-1，-1)，C(1，-1)，D(1，2)，点P从点A出发，沿长方形的边顺时针运动，速度为每秒2个单位长度，点Q从点A出发，沿长方形的边逆时针运动，速度为每秒3个单位长度．记P，Q在长方形边上第1次相遇时的点为M₁ ，第二次相遇时的点为M₂ ，第三次相遇时的点为M₃ ， …，则点M₂₀₂₂的坐标为（）

A、(1，0) B、(-1，0) C、(1，2) D、(0，-1)

查看试题解析

二、填空题

9. 已知线段AB $/ /$ y轴，若点A的坐标为（5，n-1），B（n²+1，1），则n为．

查看试题解析
10. 在平面直角坐标系xOy中，对于P、Q两点给出如下定义：如果点P到x、y轴的距离中的最小值等于点Q到x、y轴的距离中的最小值，那么称P、Q两点为“坐标轴等距点”，例如点 $P (2 ， 2)$ 与点 $Q (- 2 ， - 3)$ 为“坐标轴等距点”．已知点A的坐标为 $(- 3 ， 2)$ ，如果点B在直线 $y = x - 1$ 上，且A，B两点为“坐标轴等距点”，那么点B的坐标为．

查看试题解析
11. 在平面直角坐标系 $x O y$ 中，A，B两点的坐标如图所示，三角形 $O A B$ 的面积为．

查看试题解析
12. 如图，在平面直角坐标系中有一个点 $A (1 ， 0)$ ，点 $A$ 第一次向左跳动至 $A_{1} (- 1 ， 1)$ ，第二次向右跳动至 $A_{2} (2 ， 1)$ ，第三次向左跳动至 $A_{3} (- 2 ， 2)$ ，第四次向右跳动至 $A_{4} (3 ， 2)$ ， …，依照此规律跳动下去，点 $A$ 第2023次跳动到点 $A_{2023}$ 的坐标为

查看试题解析

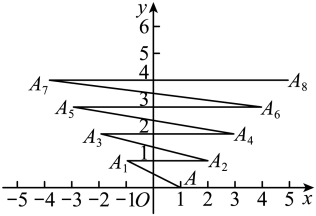
三、解答题

13. 如图，已知A(－2，0)，B(4，0)，C(2，4)．D(0，2)

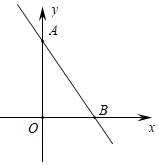
(1)、求三角形ABC的面积；

(2)、设P为坐标轴上一点，若 $S_{Δ A P C} = \frac{1}{2} S_{Δ A B C}$ ，求P点的坐标．

查看试题解析
14. 如图，在平面直角坐标系中，点A在y轴上，点B在x轴上，∠OAB＝30°．
（Ⅰ）若点C在y轴上，且△ABC为以AB为腰的等腰三角形，求∠BCA的度数；

（Ⅱ）若B（1，0），沿AB将△ABO翻折至△ABD ．请根据题意补全图形，并求点D的横坐标．

查看试题解析

四、综合题

15. 如图，直角坐标系中， $△ A B C$ 的顶点都在网格上，其中 $C$ 点坐标为 $(1 ， 2)$ ．

(1)、写出点 $A$ 、 $B$ 的坐标：

(2)、将 $△ A B C$ 先向左平移2个单位长度，再向上平移1个单位长度，得到 $△ A^{'} B^{'} C^{'}$ ，请你画出平移后的 $△ A^{'} B^{'} C^{'}$ ．

查看试题解析
16. 已知点A的坐标是 $(3 a - 14 ， a + 2)$ ，试分别根据下列条件，求出点A的坐标，

(1)、 $3 a - 14$ 和 $a + 2$ 是某正数的两个不同的平方根；

(2)、 $a + 2$ 等于 $\sqrt{7}$ 的整数部分；

(3)、点A在过点 $P (4 ， - 2)$ ，且与y轴平行的直线上．

查看试题解析

2023-2024学年初中数学沪科版八年级上册 11.1 平面内点的坐标 同步分层训练培优卷

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学沪科版八年级上册 11.1 平面内点的坐标同步分层训练培优卷