贵州省铜仁市印江土家族苗族自治县2023-2024学年七年级上学期期中数学试题

试卷更新日期：2023-12-16 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共36分。以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请用2B铅笔在答题卡相应位置作答.）

1. 中老铁路是与中国铁路网直接连通的国际铁路，线路北起中国西南地区的昆明市，南向到达老挝首都万象市，是“一带一路”上最成功的样板工程．从长期看将会使老挝每年的总收入提升21%，若+21%表示提升21%，则-10%表示（　　）

A、提升10% B、提升31% C、下降10% D、下降-10%

查看试题解析
2. 党的二十大报告中指出，我国全社会研发经费支出从一万亿元增加到二万八千亿元，居世界第二位，研发人员总量居世界首位．将2800000000000用科学记数法表示为（）

A、0.28×10¹³ B、2.8×10¹¹ C、2.8×10¹² D、28×10¹¹

查看试题解析
3. 魏晋时期的数学家刘徽在其著作《九章算术注》中用不同颜色的算筹（小棍形状的记数工具）分别表示正数和负数．如图1表示的是（+21）+（﹣32）＝﹣11的计算过程（白色为正，灰色为负），则图2表示的计算过程是（　　）

A、（﹣13）+（+23）＝+10 B、（﹣31）+（+32）＝+1 C、（+13）+（+23）＝+36 D、（+13）+（﹣23）＝﹣10

查看试题解析
4. 下列说法正确的有（）
      $①$ 相反数是它本身的数是 $0$ ；

      $②$ 绝对值是它本身的数是正数；

      $③$ 倒数是它本身的数是 $1$ ；

      $④$ 一个有理数不是整数就是分数；

      $⑤$ 数轴上距原点 $3$ 个单位的点表示的数是 $3$ ；

      $⑥$ 绝对值相等的两数互为相反数．

A、 $2$ 个 B、 $3$ 个 C、 $4$ 个 D、 $5$ 个

查看试题解析
5. 某商店上月的营业额是a万元，本月比上月增长15%，那么本月的营业额是（　　）

A、15%（a+1）万元 B、15% a万元 C、（1+15%）a万元 D、（1+15%）²a万元

查看试题解析
6. 下列判断中错误的是（　　）

A、1﹣a﹣ab是二次三项式 B、﹣a²b²c是单项式 C、 $\frac{a + b}{2}$ 是多项式 D、 $\frac{3}{4} π r^{2}$ 中，系数是 $\frac{3}{4}$

查看试题解析
7. 如图所示的程序计算，若开始输入的值为 $- \frac{1}{2}$ ，则输出的结果 $y$ 是（）

A、25 B、30 C、45 D、40

查看试题解析
8. 若|m﹣n|＝n﹣m ，且|m|＝4，|n|＝3，则m+n＝（　　）

A、1或﹣1 B、﹣1或7 C、1或﹣7 D、﹣1或﹣7

查看试题解析
9. 若x²﹣3x＝4，则3x²﹣9x+8的值是（）

A、20 B、16 C、4 D、﹣4

查看试题解析
10. 设α，β为有理数，现规定一种新运算“⊕”，满足α⊕β＝α×β+1，则2⊕（﹣3）的值是（　　）

A、5 B、7 C、﹣5 D、﹣7

查看试题解析
11. 有理数a ， b ， c在数轴上对应的点的位置如图所示，则下列各式正确的有（　　）
①abc＞0；②a+c＜b；③ $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = - 1$ ；④b＜c＜﹣a＜0＜a＜﹣c＜﹣b ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．我们知道，|a|表示数a到原点的距离，这是绝对值的几何意义．比如：|x﹣2|的几何意义是数轴上表示数x的点与表示数2的点的距离，|x+1|的几何意义是数轴上表示数x的点与表示数﹣1的点的距离．当|x+1|+|x﹣2|取得最小值时，求x的整数和是（　　）

A、﹣1 B、0 C、1 D、2

查看试题解析

二、填空题（每小题4分，共16分）

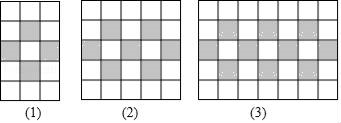
13. 比较大小：﹣2023 ﹣2024（填“＞”或“＜”）．

查看试题解析
14. 若单项式2x²y^m与 $- \frac{1}{3} x^{n} y^{4}$ 可以合并成一项，则n^m= ．

查看试题解析
15. 若|a+1|+（b﹣2）²＝0，则（a+b）²⁰²¹+a²⁰²²＝．

查看试题解析
16. 如图，图案由边长相等的黑、白两色正方形按一定规律拼接而成，第n个图案中白色正方形的个数比黑色正方形的个数多．（用含有n的代数式表示）

查看试题解析

三、解答题（本大题共9个小题，共98分，解答应写出必要的文字说明、证明过程或演算步骤）

17. 把下列各数对应的序号填在相应的大括号内．
①﹣9.3，② $\frac{3}{100}$ ， ③﹣20，④0，⑤0.01，⑥﹣1，⑦ $- \frac{7}{2}$ ， ⑧3.14，⑨100．
正数集合{ }；
整数集合{ }；
负分数集合{ }；
非负数集合{ }；
自然数集合{ }．

查看试题解析
18. 计算：

(1)、5+（﹣6）+3﹣（﹣4）；

(2)、 $- 1^{2024} - [2 - {(- 2)}^{3}] \div (- \frac{2}{5}) \times \frac{5}{2}$ ．

查看试题解析
19. 先化简，再求值：2（x²y+xy²）﹣2（x²y﹣1）﹣3xy²﹣2，其中x＝﹣2，y＝ $\frac{1}{2}$ ．

查看试题解析
20. 把下列各数在数轴上表示出来，并把它们按从小到大的顺序用“＜”号连接起来：
3，﹣（﹣1），﹣1.5，0，﹣|﹣2|， $- 3 \frac{1}{2}$ ， ﹣1⁴ ．

查看试题解析
21. 有理数a、b、c在数轴上的位置如图：

(1)、用“＞”或“＜”填空：b﹣c0，a+b0，c﹣a0．

(2)、化简：|b﹣c|+|a+b|﹣|c﹣a|

查看试题解析
22. 我省某市教育局倡导全民阅读行动，嘉淇同学坚持阅读，她每天以阅读35分钟为标准，超过的时间记作正数，不足的时间记作负数．下表是她最近一周阅读情况的记录（单位：分钟）．
星期
一
二
三
四
五
六
七
与标准的差（分钟）
+8
0
﹣10
﹣3
+2
+25
+6

(1)、星期六嘉淇阅读了分钟．

(2)、求嘉淇这周平均每天阅读的时间．

(3)、嘉淇预计从下周周一开始，阅读《数学的故事》，若嘉淇阅读该书内文的速度为每页3分钟，若她将这本书看完需要3周，且平均每天阅读的时间与（2）中相同，则这本书的内文总共有页．

查看试题解析
23. 某商店销售羽毛球拍和羽毛球，羽毛球拍每副定价40元，羽毛球每桶定价10元，“双十一”期间商店决定开展促销活动，活动期间向客户提供两种优惠方案．
方案一：买一副羽毛球拍送一桶羽毛球；
方案二：羽毛球拍和羽毛球都按定价的90%付款．
现某客户要到该商店购买羽毛球拍10副，羽毛球x桶（x＞10）．

(1)、若该客户按方案一、方案二购买，分别需付款多少元？（用含x的代数式表示）

(2)、当x＝30时，通过计算，说明此时按哪种方案购买较为合算？

(3)、当x＝30时，你还能给出一种更为省钱的购买方案吗？试写出你的购买方法，并计算需付款多少元？

查看试题解析
24. 已知多项式A和B ，且2A+B＝7ab+6a﹣2b﹣11，2B﹣A＝4ab﹣3a﹣4b+18．
阅读材料：我们总可以通过添加括号的形式，求出多项式A和B ．如：
5B＝（2A+B）+2（2B﹣A）
＝（7ab+6a﹣2b﹣11）+2（4ab﹣3a﹣4b+18）
＝15ab﹣10b+25
∴B＝3ab﹣2b+5

(1)、应用材料：请用类似于阅读材料的方法，求多项式A ．

(2)、小红取a ， b互为倒数的一对数值代入多项式A中，恰好得到A的值为0，求多项式B的值．

(3)、聪明的小刚发现，只要字母b取一个固定的数，无论字母a取何数，B的值总比A的值大7，那么小刚所取的b的值是多少呢？

查看试题解析
25. [概念学习]
规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如2÷2÷2等．类比有理数的乘方，我们把2÷2÷2记作2₃ ，读作“2的下3次方”，一般地，把n个a（a≠0）相除记作a_n ，读作“a的下n次方”．
[初步探究]

(1)、直接写出计算结果：2₃＝．

(2)、关于除方，下列说法正确的选项有（只需填入正确的序号）；
①任何非零数的下2次方都等于1；
②对于任何正整数n ， 1_n＝1；
③3₄＝4₃；
④负数的下奇数次方结果是负数，负数的下偶数次方结果是正数．

(3)、【深入思考】
我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢？
例如：2₄＝2÷2÷2÷2＝2× $\frac{1}{2}$ × $\frac{1}{2}$ × $\frac{1}{2}$ ＝ ${(\frac{1}{2})}^{2}$ （幂的形式）；
试一试：将下列除方运算直接写成幂的形式.5₆＝； ${(- \frac{1}{2})}_{10}$ ＝；

(4)、算一算： ${(- \frac{1}{4})}_{4}$ ÷2³+（﹣8）×2₃ ．

查看试题解析

星期	一	二	三	四	五	六	七
与标准的差（分钟）	+8	0	﹣10	﹣3	+2	+25	+6