山东省济南市天桥区2023-2024学年九年级上学期期中考试数学试题

试卷更新日期：2023-12-16 类型：期中考试

进入出卷网下载

一、选择题（本大题共10个小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 如图是一个零件的示意图，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
2. 已知2a=3b(ab≠0)，则下列比例式成立的是（）

A、 $\frac{a}{2}$ = $\frac{3}{b}$ B、 $\frac{a}{3}$ = $\frac{b}{2}$ C、 $\frac{a}{b}$ = $\frac{2}{3}$ D、 $\frac{b}{a}$ = $\frac{3}{2}$

查看试题解析
3. 如图，两条直线被三条平行线所截，若DE=3，EF=6，BC=8，则AB等于（）

A、4 B、8 C、12 D、9

查看试题解析
4. 若x=1是关于x的一元二次方程x²－mx+3=0的一个解，则m的值是（）

A、6 B、5 C、4 D、3

查看试题解析
5. 若反比例函数y= $\frac{6}{x}$ 的图像经过点（﹣2，a），则a的值是（）

A、6 B、﹣2 C、﹣3 D、3

查看试题解析
6. 下列命题正确的是（）

A、对角线相等的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线互相垂直的平行四边形是菱形 D、对角线互相垂直且相等的四边形是正方形

查看试题解析
7. 对于反比例函数y=﹣ $\frac{2}{x}$ ，下列说法不正确的是（）

A、图象分布在第二、四象限 B、图象关于原点对称 C、图象经过点（1，﹣2） D、若点A(x₁ ， y₁)，B(x₂ ， y₂）都在该函数图象上，且x₁<x₂ ，则y₁<y₂

查看试题解析
8. 如图，在平行四边形 $A B C D$ 中，点E在边 $D C$ 上， $D E ： E C ＝ 4 ： 1$ ，连接 $A E$ 交 $B D$ 于点F，则 $△ D E F$ 的面积与 $△ B A F$ 的面积之比为（）

A、 $4 ： 5$ B、 $9 ： 16$ C、 $16 ： 25$ D、 $3 ： 5$

查看试题解析
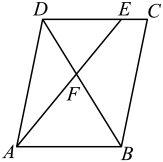9. 电影《长安三万里》上映以来，全国票连创佳绩，据不完全统计，某市第一天票房约2亿元，若以后每天票房按相同的增长率增长，三天后累计票房收入达10亿元，将增长率记作x，则方程可以列为（）

A、(1+x)²=10 B、2(1+x)²=10 C、2+2x+2(1+x)²=10 D、2+2(1+x)+2(1+x)²=10

查看试题解析
10. 如图，在矩形ABCD中，点F是CD边上的一点，把矩形ABCD沿BF折叠，点C落在AD边上的点E处，AD=5，AB=4，点M是线段CF上的动点，连接BM，过点E作BM的垂线交BC于点N，垂足为H．以下结论：①△ABE∽△DEF：② $\frac{A E}{B E}$ = $\frac{D E}{E F}$ ：③CF=2：④ $\frac{B M}{E N}$ = $\frac{5}{4}$ .其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题：（本大题共6个小题，每小题4分，共24分）

11. 一元二次方程x²=x的根是.

查看试题解析
12. 若 $\frac{a}{2}$ ＝ $\frac{b}{3}$ ，则 $\frac{a + b}{b}$ =.

查看试题解析
13. 为了估计水塘中的鱼数，养鱼者先从鱼塘中捕获50条鱼，在每一条鱼身上做好标记后把这些鱼放归鱼塘，再从鱼塘中打捞鱼．通过多次实验后发现捕捞的鱼中有作记号的频率稳定在2.5%左右，则鱼塘中估计有鱼条．

查看试题解析
14. 如图的红叶，A，B，C三点在同一直线上，B为AC的黄金分割点（AB>BC)，若AC的长度为10cm，则BC的长度为.（结果保留根号）

查看试题解析
15. 如图，是反比例函数y= $\frac{k_{1}}{x}$ 和y= $\frac{k_{2}}{x}$ （k₁<k₂）在第一象限的图象，直线AB//x轴，并分别交两条曲线于A、B两点，若S_A_OB=2，则k₂－k₁的值是.

查看试题解析
16. 如图，正方形ABCD边长为4，O为对角线BD的中点，点M在边AB上，且BM=2AM，点N在边BC上，且BN=AM，连接AN，MD交于点P，连接OP，则OP的长为.

查看试题解析

三、解答题（本大题10个小题，共86分．解答应写出文字说明、证明过程或演算步骤）

17. 解方程： $x^{2} + 4 x + 3 = 0$ .

查看试题解析
18. 如图，四边形ABCD是菱形，AE⊥BC于点E，AF⊥CD于点F.求证：△ABE≌△ADF.

查看试题解析
19. 如图，某同学利用镜面反射的原理巧妙地测出了树的高度，已知人的站位点A，镜子点O，树底点B三点在同一水平线上，眼睛与地面的高度为1.6米，OA =2.4米，OB=6米，则树高为多少米．

查看试题解析
20. 如图，在△ABC中，∠CAD=∠B，BC=8，D是BC边上一点，且CD=2.

(1)、求证：△ABC∽△DAC.

(2)、求AC的长．

查看试题解析
21. 在如图的方格纸中（每个小方格都是边长为1个单位长度的正方形），△OAB的顶点坐标分别为O(0，0)，A(﹣2，﹣1)，B(﹣1，﹣3)，△O₁A₁B₁与△OAB是关于点P为位似中心的位似图形．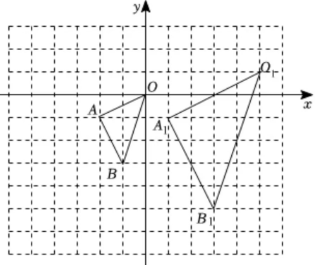

(1)、在图中标出位似中心P的位置并直接写出P点的坐标.

(2)、以原点O为位似中心，在位似中心的同侧画出△OAB的一个位似△OA₂B₂ ，使它与△OAB的位似比为2：1.

(3)、△OAB的内部一点M的坐标为（a，b），直接写出点M在△OA₂B₂中的对应点M₂的坐标为.

查看试题解析
22. 有甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2；乙袋中装有3个完全相同的小球，分别标有数字﹣1，﹣2，0；现从甲袋中随机抽取一个小球，记录标有的数字为x，再从乙袋中随机抽取一个小球，记录标有的数字为y，确定点M的坐标为（x，y）.

(1)、用树状图或列表法列举点M所有可能的坐标.

(2)、求点M(x，y)在函数y=﹣x+1的图象上的概率．

查看试题解析
23. 如图，学校打算用16m的篱笆围成一个长方形的生物园饲养小兔，生物园的一面靠墙，墙长8m，长方形的面积是30m² ．求生物园的长和宽．

查看试题解析
24. 如图，在Rt△ABC中，∠ACB=90°，AC=4cm，BC=3cm，点P由点B出发沿BA方向向点A匀速运动，速度为1cm/s，同时点Q由A出发沿AC方向向点C匀速运动，速度为1cm/s，连接PQ．设运动的时间为t(s)，其中0<1<4．解答下列问题：

(1)、AP= ， AQ＝（用含t的代数式表示）

(2)、当t为何值时，△APQ∽△ABC.

(3)、在P、Q运动过程中，是否存在某一时刻使得PC=PQ，若能，求出此时t的值；若不能，请说明理由．

查看试题解析
25. 如图，已知一次函数图象y=x+b与y轴交于点C(0，1)，与反比例函数图象y= $\frac{k}{x}$ 交于点A(a，2)和点B两点．

(1)、求一次函数和反比例函数的解析式.

(2)、求点B的坐标和△AOB的面积.

(3)、若点M为y轴上的一个动点，N为平面内任意一点，当四边形ABMN是矩形时，请求出M点坐标．

查看试题解析
26. 已知△ABC中，∠ABC=90°，点D、E分别在边BC、边AC上，连接DE，DF⊥DE，点F、点C在直线DE同侧，连接FC，且 $\frac{A B}{B C}$ = $\frac{D E}{D F}$ =k.

(1)、点D与点B重合时：
①如图1，k=1时，AE和FC的数量关系是 ▲ ，位置关系是 ▲ .
②如图2，k=2时，猜想AE和FC的关系，并说明理由；

(2)、BD=2CD时，
①如图3，k =1时，若AE=2，S_△_CDF=6，求FC的长度.
②如图4，k=2时，点M、N分别为EF和AC的中点，若AB=10，直接写出MN最小值．

查看试题解析